
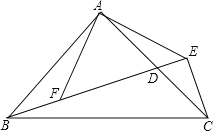
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,BE⊥CE,垂足是E,BE交AC于点D,F是BE上一点,AF⊥AE,且C是线段AF的垂直平分线上的点,AF=2![]() ,则DF=________.
,则DF=________.
【答案】3.
【解析】
由题意可证的△ABF≌△ACE,可得△AEF为等腰直角三角形,取AF的中点O,连接CO交BE与点G,连接AG,可得△AGF, △AGE,△CEG均为等腰直角三角形,可得AG平行等于CE,可得四边形AGCE为平行四边形,可得FD的长.
解:如图
![]() Rt△ABC中,AB=AC,∠BAC=90°,
Rt△ABC中,AB=AC,∠BAC=90°,![]() ∠ABC=∠ACB=45°,
∠ABC=∠ACB=45°,
又![]() ∠BAC=90°,BE⊥CE,∠DAE为∠BAC与EAF的公共角
∠BAC=90°,BE⊥CE,∠DAE为∠BAC与EAF的公共角
![]() ∠BAF=∠CAE,
∠BAF=∠CAE,
![]() ∠ABC=∠ACB=45°, BE⊥CE
∠ABC=∠ACB=45°, BE⊥CE
![]() ∠ABF+∠CBE=45°,∠CBE+∠ACB+∠ACE=90°,即: ∠CBE+∠ACE=45°,
∠ABF+∠CBE=45°,∠CBE+∠ACB+∠ACE=90°,即: ∠CBE+∠ACE=45°,
![]() ∠ABF=∠ACE,
∠ABF=∠ACE,
在△ABF与△ACE中,有
 ,
,![]() △ABF≌△ACE,
△ABF≌△ACE,
![]() AE=AF, △AEF为等腰直角三角形, 取AF的中点O,连接CO交BE与点G,连接AG,
AE=AF, △AEF为等腰直角三角形, 取AF的中点O,连接CO交BE与点G,连接AG,
![]() C是线段AF的垂直平分线上的点,易得△AGF, △AGE,△CEG均为等腰直角三角形,
C是线段AF的垂直平分线上的点,易得△AGF, △AGE,△CEG均为等腰直角三角形,
![]() AF=2
AF=2![]()
![]() AG=GE=CE=FG=2,
AG=GE=CE=FG=2,
又AG⊥BE,CE⊥BE,可得AG∥CE,
![]() 四边形AGCE为平行四边形,
四边形AGCE为平行四边形,
![]() GD=DE=1,
GD=DE=1,
![]() DF=FG+GD=2+1=3.
DF=FG+GD=2+1=3.


科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚同学动手剪了如图①所示的正方形与长方形纸片若干张.

(1)他用1张1号、1张2号和2张3号卡片拼出一个新的图形(如图②).根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是 ;
(2)如果要拼成一个长为(a+2b),宽为(a+b)的大长方形,则需要2号卡片 张,3号卡片 张;
(3)当他拼成如图③所示的长方形,根据6张小纸片的面积和等于打纸片(长方形)的面积可以把多项式a2+3ab+2b2分解因式,其结果是 ;
(4)动手操作,请你依照小刚的方法,利用拼图分解因式a2+5ab+6b2= 画出拼图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
(1)先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为 , 若A为随机事件,则m的取值为;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E. 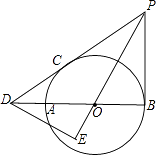
(1)求证:∠DPO=∠EDB;
(2)若PB=3,DB=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
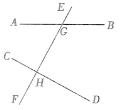
【题目】如图,直线AB,CD被直线EF所截,交点分别为G,H, ∠CHG=∠DHG=![]() ∠AGE.
∠AGE.
(1)CD与EF有怎样的位置关系?请说明理由.
(2)求∠CHG的同位角、内错角、同旁内角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依次规律,第6个图形的小圆个数是( )

A. 56 B. 54 C. 44 D. 42
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )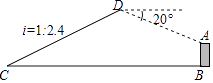
A.29.1米
B.31.9米
C.45.9米
D.95.9米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com