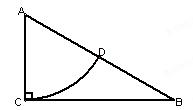
1、∵MN⊥AB,
∴∠MAC+∠CAB=90°
∵AB是半圆直径,
∴∠ACB=90°
∴∠CAB+∠ABC=90°,
∵∠ABC=∠MAC,(已知),
∴∠MAC+∠CAB=90°,
∴MN是半圆的切线。
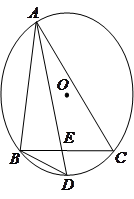
2、∵D是弧AC的中点,
∴BD是∠CBA的平分线,
∠CBD=∠DBA,
∠CGB=90°-∠CBA,
∵∠DGF=∠CGB(对顶角相等),
∴∠DGF=90°-∠CBD,
∵DE⊥AB,
∴∠GDF=90°-∠DBE,
∴∠EDG=∠DGF,
∴△FDG是等腰△,
∴FD=FG。
3、作FP⊥DG,
S△FDG=9/2,
DG=3,
S△FDG=DG*FP/2,
FP=3,
∵∠PGF=∠CGB(对顶角相等),
∠BCG=∠GPE=90°
∴△BGC∽△FGP,
FP/BC=PG/CG,PG=DG/2=3/2,
3/BC=(3/2)/4,
BC=8,
∴S△BGC=BC*CG/2=8*4/2=16