
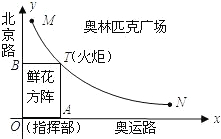
��ͼ������ʥ��ִ�ij�а���ƥ�˹㳡����ͼ��ֱ������ϵ�е�һ�η���������ͼ�ݣ�����T��m��n����ʾ���λ�ã������뱱��·10�״���M�㿪ʼ���ݣ����뱱��·1000��N��ʱ���ݻ������ӭʥ����ʱָ�Ӳ���������ԭ��O������·�����·��ʮ��·�ڣ���OATBΪ���ȶ�Ա�ʻ�������ʼ�ձ��־�����״�������Ϊ10000ƽ���ף�·�߿��Ⱦ����ƣ���

��1����ͼ�з����������Ĺ�ϵʽ������д���Ա�����ȡֵ��Χ����
��2�����ʻ�������ܳ�Ϊ500��ʱ��ȷ����ʱ����λ�ã��������ʾ����
��3����t=m��n���ú�t�Ĵ���ʽ��ʾ��浽ָ�Ӳ��ľ��룻�������ָ�Ӳ����ʱ��ȷ����ʱ����λ�ã��������ʾ����
��1�� ��2����50��200����200��50�� ��3��T��100��100��
��2����50��200����200��50�� ��3��T��100��100��
��������
������������ȸ������⣬����ʥ��ִ�ij�а���ƥ�˹㳡����ͼ��ֱ������ϵ�е�һ�η���������ͼ�ݣ��ҷ���ʼ�ձ��־�����״�������Ϊ10000ƽ���ף��������ݴ����ô���ϵ�����ɵ÷����������Ĺ�ϵʽ����һ�����ɵô𰸣�
�⣺��1���跴��������Ϊ ��k��0����
��k��0����
��k=xy=mn=S����OATB=10000��
�� ��
��
��2�����ʻ�����ij�Ϊm�ף����Ϊ��250��m���ף��������
m��250��m��=10000��
250m��m2=10000��
��m2��250m+10000=0��
���m=50��m=200���������⣮
���ʱ��������Ϊ��50��200����200��50����
��3����mn=10000����Rt��TAO��
 =
= ��
��
�൱t=0ʱ��TO��С��
��t=m��n��
���ʱm=n����mn=10000��m��0��n��0��
��m=n=100����10��100��1000��
��T��100��100����
���㣺������������Ӧ�ã�
��������ʵ�����д��ڴ����ɷ�������������������������������Ĺؼ���ȷ����������֮��ĺ�����ϵ��Ȼ�����ô���ϵ����������ǵĹ�ϵʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 000ƽ���ף�·�߿��Ⱦ����ƣ���
000ƽ���ף�·�߿��Ⱦ����ƣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �Ⱦ����ƣ���
�Ⱦ����ƣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 0000ƽ���ף�·�߿��Ⱦ����ƣ���
0000ƽ���ף�·�߿��Ⱦ����ƣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010-2011ѧ���㽭ʡ�������²���ѧ���꼶���ϣ�������ѧģ���Ծ�3�������棩 ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com