
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC= ![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
【答案】
(1)
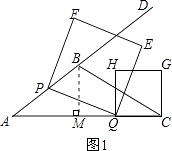
解:如图1,过点B作BM⊥AC于点M,
∵AC=9,S△ABC= ![]() ,
,
∴ ![]() ACBM=
ACBM= ![]() ,即
,即 ![]() ×9BM=
×9BM= ![]() ,
,
解得BM=3.
由勾股定理,得
AM= ![]() =
= ![]() =4,
=4,
则tanA= ![]() =
= ![]() ;
;
(2)
存在.
如图2,过点P作PN⊥AC于点N.
依题意得AP=CQ=5t.
∵tanA= ![]() ,
,
∴AN=4t,PN=3t.
∴QN=AC﹣AN﹣CQ=9﹣9t.
根据勾股定理得到:PN2+NQ2=PQ2,
S正方形PQEF=PQ2=(3t)2+(9﹣9t)2=90t2﹣162t+81(0<t< ![]() ).
).
∵﹣ ![]() =
= ![]() =
= ![]() 在t的取值范围之内,
在t的取值范围之内,
∴S最小值= ![]() =
= ![]() =
= ![]()
(3)
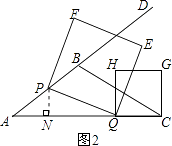
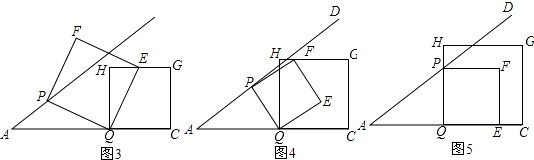
①如图3,当点E在边HG上时,t1= ![]() ;②如图4,当点F在边HG上时,t2=
;②如图4,当点F在边HG上时,t2= ![]() ;③如图5,当点P边QH(或点E在QC上)时,t3=1④如图6,当点F边CG上时,t4=
;③如图5,当点P边QH(或点E在QC上)时,t3=1④如图6,当点F边CG上时,t4= ![]() .
.
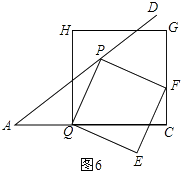
【解析】(1)如图1,过点B作BM⊥AC于点M,利用面积法求得BM的长度,利用勾股定理得到AM的长度,最后由锐角三角函数的定义进行解答;(2)如图2,过点P作PN⊥AC于点N.利用(1)中的结论和勾股定理得到PN2+NQ2=PQ2 , 所以由正方形的面积公式得到S关于t的二次函数,利用二次函数的顶点坐标公式和二次函数图象的性质来求其最值;(3)需要分类讨论:当点E在边HG上、点F在边HG上、点P边QH(或点E在QC上)、点F边C上时相对应的t的值.


科目:初中数学 来源: 题型:
【题目】如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离( ![]() 取1.73,结果精确到0.1千米)
取1.73,结果精确到0.1千米) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
组别 | 分数段 | 频数(人) | 频率 |
1 | 50≤x<60 | 30 | 0.1 |
2 | 60≤x<70 | 45 | 0.15 |
3 | 70≤x<80 | 60 | n |
4 | 80≤x<90 | m | 0.4 |
5 | 90≤x<100 | 45 | 0.15 |

请根据以图表信息,解答下列问题:
(1)表中m= , n=;
(2)补全频数分布直方图;
(3)在得分前5名的同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学参加区级的比赛,用树状图或列表法求选出的两名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: 
(1)李老师一共调查了多少名同学?
(2)C类女生有3名,D类男生有1名,将图1条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:
①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形;
③四边形CDFE的面积保持不变;
④△CDE面积的最大值为8.
其中正确的结论有( )个.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD, 
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年5月31日,我国飞人苏炳添在美国尤金举行的国际田联钻石联赛100米男子比赛中,获得好成绩,成为历史上首位突破10秒大关的黄种人.如表是苏炳添近五次大赛参赛情况:
比赛日期 | 2012﹣8﹣4 | 2013﹣5﹣21 | 2014﹣9﹣28 | 2015﹣5﹣20 | 2015﹣5﹣31 |
比赛地点 | 英国伦敦 | 中国北京 | 韩国仁川 | 中国北京 | 美国尤金 |
成绩(秒) | 10.19 | 10.06 | 10.10 | 10.06 | 9.99 |
则苏炳添这五次比赛成绩的众数和平均数分别为( )
A.10.06秒,10.06秒
B.10.10秒,10.06秒
C.10.06秒,10.08秒
D.10.08秒,10.06秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆准备购进一批换气扇,从电器商场了解到:一台A型换气扇和三台B型换气扇共需275元;三台A型换气扇和二台B型换气扇共需300元.
(1)求一台A型换气扇和一台B型换气扇的售价各是多少元;
(2)若该宾馆准备同时购进这两种型号的换气扇共40台并且A型换气扇的数量不多于B型换气扇数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com