
在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
(1)如图1,当点G在BC边上时,易证:PG=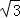 PC.(不必证明)
PC.(不必证明)
(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,写出你的猜想(不必证明).
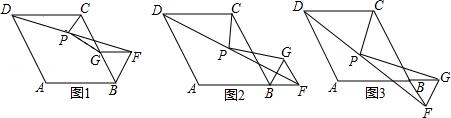
(2)猜想:PG=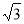 PC,证明见解析
PC,证明见解析
(3)猜想:PG=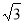 PC
PC
【解析】
试题分析:(2)延长GP交DA于点E,连接EC,GC,先证明△DPE≌△FPG,再证得△CDE≌△CBG,利用在Rt△CPG中,∠PCG=60°,所以PG=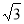 PC.
PC.
(3)PG= PC.
PC.
试题解析:(2)猜想:PG=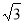 PC
PC
如图2,延长GP交DA于点E,连接EC,GC,
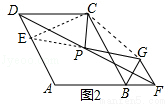
∵∠ABC=60°,△BGF正三角形
∴GF//BC//AD,
∴∠EDP=∠GFP,
又∵DP=FP,∠DPE=∠FPG
∴△DPE≌△FPG(ASA)
∴PE=PG,DE=FG=BG,
∵∠CDE=CBG=60°,CD=CB,
∴△CDE≌△CBG(SAS)
∴CE=CG,∠DCE=∠BCG,
∴∠ECG=∠DCB=120°,
∵PE=PG,
∴CP⊥PG,∠PCG=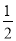 ∠ECG=60°
∠ECG=60°
∴PG=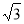 PC.
PC.
(3)猜想:PG=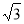 PC.
PC.
考点:1、全等三角形的判定;2、菱形的性质;3、等边三角形的性质


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014年初中毕业升学考试(黑龙江龙东卷)数学(解析版) 题型:解答题
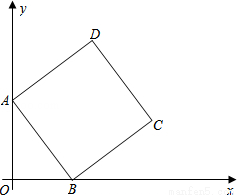
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).
(1)求点D的坐标.
(2)求直线BC的解析式.
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江龙东卷)数学(解析版) 题型:选择题
下列各运算中,计算正确的是( )
A.4a2﹣2a2=2 B.(a2)3=a5 C.a3•a6=a9 D.(3a)2=6a2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江绥化卷)数学(解析版) 题型:解答题
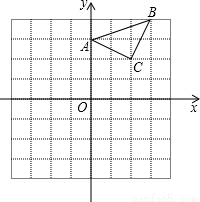
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江牡丹江卷)数学(解析版) 题型:解答题
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图,请结合图象信息解答下列问题:

(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)两车出发后几小时相距的路程为200千米?请直接写出答案.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:填空题
某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为 人.(注:横轴上每组数据包含最小值不包含最大值)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com