(A类)
在这次抗震救灾募捐活动中,某班共捐款1400元.班委会决定,由小敏、小聪两人负责选购圆珠笔、钢笔共800支,送给结对的灾区学校的同学,他们去了国商大厦,看到圆珠笔每支1.5元,钢笔(中性笔)每支2元.
(1)若他们购买圆珠笔、钢笔刚好用去1400元,问圆珠笔、钢笔各买了多少支?
(2)若购买圆珠笔可9折优惠,购买钢笔可8折优惠,这样购买(1)中一样多的圆珠笔和钢笔后还可余下多少钱若用余下的钱先买了80支圆珠笔后,还能买多少支钢笔?
(B类)
(1)如图1,在△ABC中,∠ABC和∠ACB的平分线交于点O.则有∠BOC=
90°+∠A,请说明理由;
(2)如图2,在△ABC中,内角∠ABC的平分线和外角∠ACD的平分线交于点O.请直接写出∠BOC与∠BAC的关系,不必说明理由;
(3)如图3,AP、BP分别平分∠CAD、∠CBD.则有∠P=
(∠C+∠D),请说明理由;
(4)如图4,AP、BP分别平分∠CAM、∠CBD.请直接写出∠P与∠C、∠D的关系,不必说明理由.

解:我选做的是
类题.

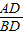 =
=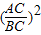 ,则△ABC是( )
,则△ABC是( )