
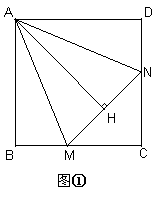
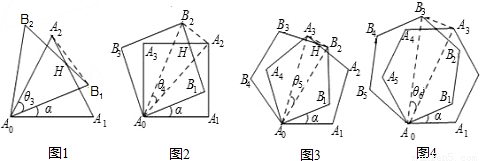
解:(1)如图①AH=AB
 (2)数量关系成立.如图②,延长CB至E,使BE=DN
(2)数量关系成立.如图②,延长CB至E,使BE=DN
∵ABCD是正方形
∴AB=AD,∠D=∠ABE=90°
∴Rt△AEB≌Rt△AND
∴AE=AN,∠EAB=∠NAD
∴∠EAM=∠NAM=45°
∵AM=AM
∴△AEM≌△ANM
∵AB、AH是△AEM和△ANM对应边上的高,
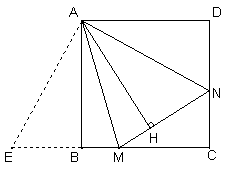 ∴AB=AH
∴AB=AH
(3)如图③分别沿AM、AN翻折△AMH和△ANH,
得到△ABM和△AND
∴BM=2,DN=3,∠B=∠D=∠BAD=90°
分别延长BM和DN交于点C,得正方形ABCE.
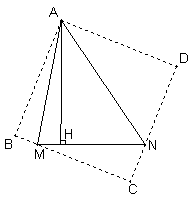 由(2)可知,AH=AB=BC=CD=AD.
由(2)可知,AH=AB=BC=CD=AD.
设AH=x,则MC=![]() , NC=
, NC=![]() 图②
图②
在Rt⊿MCN中,由勾股定理,得
![]()
∴![]()
解得![]() .(不符合题意,舍去)
.(不符合题意,舍去)
∴AH=6.
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
 29、如图,已知点D、E为△ABC的边BC上两点.AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.
29、如图,已知点D、E为△ABC的边BC上两点.AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.查看答案和解析>>
科目:初中数学 来源: 题型:
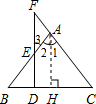 (1)如图,在△ABC中,AB=AC,D是底边BC上的一点,过点D作BC的垂线,交AB于点E,交AC的延长线于F,则△AEF是等腰三角形.请在解答过程中的括号里填写理由.
(1)如图,在△ABC中,AB=AC,D是底边BC上的一点,过点D作BC的垂线,交AB于点E,交AC的延长线于F,则△AEF是等腰三角形.请在解答过程中的括号里填写理由.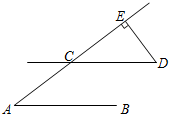
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
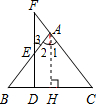 (1)如图,在△ABC中,AB=AC,D是底边BC上的一点,过点D作BC的垂线,交AB于点E,交AC的延长线于F,则△AEF是等腰三角形.请在解答过程中的括号里填写理由.
(1)如图,在△ABC中,AB=AC,D是底边BC上的一点,过点D作BC的垂线,交AB于点E,交AC的延长线于F,则△AEF是等腰三角形.请在解答过程中的括号里填写理由.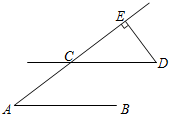
查看答案和解析>>
科目:初中数学 来源:2010年江西省赣州市定南三中初三毕业班教师专业考试数学试卷(解析版) 题型:解答题
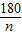 °);
°);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com