
【题目】如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题: 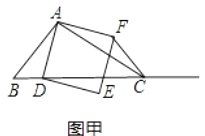
(1)如果AB=AC,∠BAC=90°, ①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 , 数量关系为 .
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?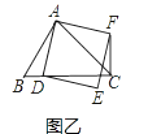
(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?并说明理由.
【答案】
(1)垂直;相等;解:成立,理由如下: ∵∠FAD=∠BAC=90°
∴∠BAD=∠CAF
在△BAD与△CAF中,
∵ 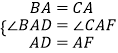
∴△BAD≌△CAF(SAS)
∴CF=BD,∠ACF=∠ACB=45°,
∴∠BCF=90°
∴CF⊥BD
(2)解:当∠ACB=45°时可得CF⊥BC,理由如下:
过点A作AC的垂线与CB所在直线交于G
则∵∠ACB=45°
∴AG=AC,∠AGC=∠ACG=45°
∵AG=AC,AD=AF,
∵∠GAD=∠GAC﹣∠DAC=90°﹣∠DAC,∠FAC=∠FAD﹣∠DAC=90°﹣∠DAC,
∴∠GAD=∠FAC,
∴△GAD≌△CAF(SAS)
∴∠ACF=∠AGD=45°
∴∠GCF=∠GCA+∠ACF=90°
∴CF⊥BC

【解析】解:(1)①CF⊥BD,CF=BD 所以答案是:垂直、相等.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
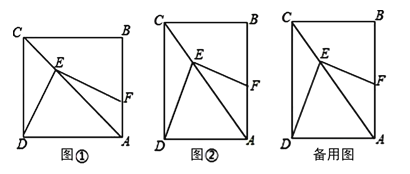
【题目】(本题满分9分)小明一直对四边形很感兴趣,在矩形ABCD中,E是AC上任意一点,连接DE,作DE⊥EF,交AB于点F.请你跟着他一起解决下列问题:
(1)如图①,若AB=BC,则DE,EF有什么数量关系?请给出证明.
(2)如图②,若∠CAB=30°,则DE,EF又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果在矩形ABCD中,BC=mAB,那DE,EF有什么数量关系?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=![]() (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点P,在公路1上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,一辆轿车在公路1上由B向A匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由(参考数据: ![]() =1.41,
=1.41, ![]() =1.73).
=1.73). 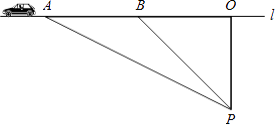
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com