
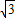 ,0),⊙M的切线OC与直线AB交于点C.
,0),⊙M的切线OC与直线AB交于点C.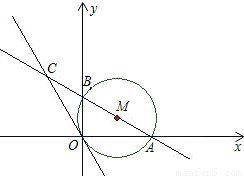
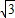 ,∠OAC=∠OCA=30°,因此∠COD=60°,因此可求出CD,OD的长,也就求出了C的坐标,可用待定系数法求出正比例函数的函数式.
,∠OAC=∠OCA=30°,因此∠COD=60°,因此可求出CD,OD的长,也就求出了C的坐标,可用待定系数法求出正比例函数的函数式.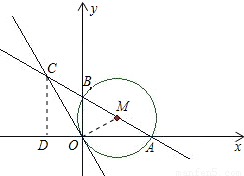 解:(1)AB=2,OA=
解:(1)AB=2,OA=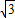 OB=
OB=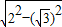 =1,
=1,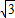 ,∠OAC=∠OCA=30°,
,∠OAC=∠OCA=30°,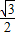 ,CD=
,CD= ,
,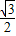 ,
, ),
),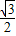 k=
k= ,
,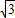 ,
,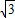 x.
x.

科目:初中数学 来源:2010年广东省广州市广雅实验中学中考数学一模试卷(解析版) 题型:选择题


查看答案和解析>>
科目:初中数学 来源:2010年广东省广州市广雅实验中学中考数学一模试卷(解析版) 题型:选择题




查看答案和解析>>
科目:初中数学 来源:2010年北京市实验外国语学校中考数学模拟试卷(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2009年内蒙古赤峰市克什克腾旗九年级下学期数学模拟试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com