
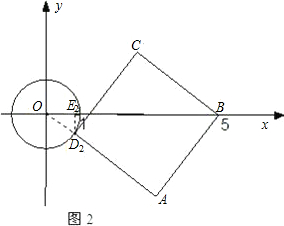
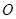 的半径为
的半径为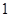 ,正方形
,正方形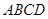 顶点
顶点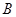 坐标为
坐标为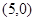 ,顶点
,顶点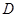 在⊙
在⊙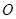 上运动.
上运动.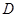 运动到与点
运动到与点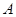 、
、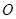 在同一条直线上时,试证明直线
在同一条直线上时,试证明直线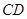 与⊙
与⊙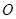 相切;
相切;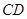 与⊙
与⊙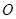 相切时,求
相切时,求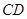 所在直线对应的函数关系式;
所在直线对应的函数关系式;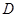 的横坐标为
的横坐标为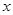 ,正方形
,正方形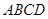 的面积为
的面积为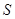 ,求
,求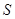 与
与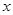 之间的函数关系式,并求出
之间的函数关系式,并求出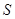 的最大值与最小值.
的最大值与最小值.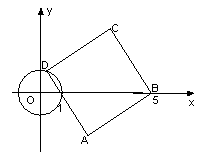
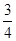 x+
x+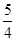 或y=
或y=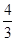 x-
x-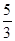 ;(3)S=13-5x,18,8.
;(3)S=13-5x,18,8.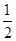 BD2=(26-10x)=13-5x;再根据x的范围可得面积的最大最小值.
BD2=(26-10x)=13-5x;再根据x的范围可得面积的最大最小值.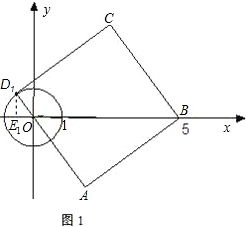
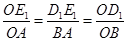 ,
,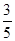 ,D1E1=
,D1E1=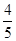 ,
,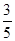 ,
,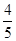 ).
).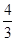 x.
x.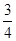 x+b,
x+b,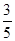 ,
,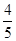 )代入解析式得b=
)代入解析式得b=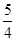 ;
;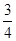 x+
x+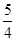 .
.
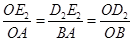 ,
,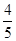 ,D2E2=
,D2E2=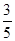 ,
,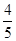 ,?
,?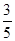 ),
),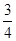 x.
x.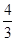 x+b,
x+b,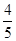 ,?
,?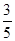 )代入解析式得b=-
)代入解析式得b=-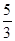 ;
;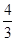 x-
x-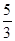 .
.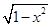 ,
,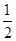 BD2=
BD2=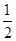 (26-10x)=13-5x,
(26-10x)=13-5x,

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源:不详 题型:解答题
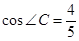 ,DF=9,求⊙O的半径。
,DF=9,求⊙O的半径。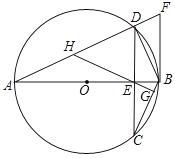
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
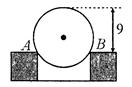
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com