练习册

  • 练习册
  • 试题
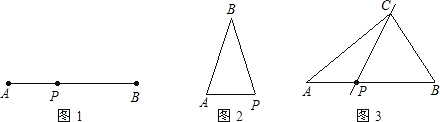
    精英家教网 > 初中数学 > 题目详情

    如图，C为AB的黄金分割点（AC＞BC），若AB的长为10，则AC的长为________．

    5-5
    分析：根据黄金分割点的定义，知AC为较长线段；则AC=AB，代入数据即可得出AC的值．
    解答：由于C为线段AB=10的黄金分割点，
    且AC＞BC，AC为较长线段；
    则AC=10×=5-5．
    故答案为：5-5．
    点评：理解黄金分割点的概念．特别注意这里的AC是较长线段，熟记黄金比的值进行计算．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （如图1），点P将线段AB分成一条较小线段AP和一条较大线段BP，如果
    AP
    BP
    =
    BP
    AB
    ，那么称点P为线段AB的黄金分割点，设
    AP
    BP
    =
    BP
    AB
    =k，则k就是黄金比，并且k≈0.618．
    精英家教网
    （1）以图1中的AP为底，BP为腰得到等腰△APB（如图2），等腰△APB即为黄金三角形，黄金三角形的定义为：满足
    底
    腰
    =
    腰
    底+腰
    ≈0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：
     
    ；
    （2）如图1，设AB=1，请你说明为什么k约为0.618；
    （3）由线段的黄金分割点联想到图形的“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分（设S1＜S2），如果
    S1
    S2
    =
    S2
    S
    ，那么称直线l为该图形的黄金分割线．（如图3），点P是线段AB的黄金分割点，那么直线CP是△ABC的黄金分割线吗？请说明理由；
    （4）图3中的△ABC的黄金分割线有几条？

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图，以矩形ABCD的宽为边在其内部作正方形AEFD．若BC与AB的比为黄金比，那么小矩形BCFE 的宽与长的比也是黄金比吗? 为什么?

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

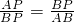    （如图1），点P将线段AB分成一条较小线段AP和一条较大线段BP，如果数学公式，那么称点P为线段AB的黄金分割点，设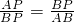数学公式=k，则k就是黄金比，并且k≈0.618．

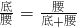    （1）以图1中的AP为底，BP为腰得到等腰△APB（如图2），等腰△APB即为黄金三角形，黄金三角形的定义为：满足数学公式≈0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：______；
    （2）如图1，设AB=1，请你说明为什么k约为0.618；
    （3）由线段的黄金分割点联想到图形的“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分（设S1＜S2），如果数学公式，那么称直线l为该图形的黄金分割线．（如图3），点P是线段AB的黄金分割点，那么直线CP是△ABC的黄金分割线吗？请说明理由；
    （4）图3中的△ABC的黄金分割线有几条？

    查看答案和解析>>

    科目：初中数学 来源：河北省模拟题 题型：解答题

    如图，△ABC为某县正在建设的黄金三角商业区，其中AC、BC为商业街，AB 为步行街，且ACB =2B.
    (1)请在步行街AB上建一路口D，使D到商业街AC、BC 的距离相等(尺规作图. 保留作图痕迹.不写作法)；
    (2)在(1)的基础上过D点作DE⊥BC，垂足为 E，请写出三种不同的结论。

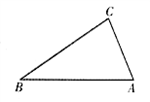
    查看答案和解析>>

    科目：初中数学 来源：2008-2009学年江苏省南京市九年级（下）教学质量检测数学试卷（解析版） 题型：解答题

    （如图1），点P将线段AB分成一条较小线段AP和一条较大线段BP，如果，那么称点P为线段AB的黄金分割点，设=k，则k就是黄金比，并且k≈0.618．

    （1）以图1中的AP为底，BP为腰得到等腰△APB（如图2），等腰△APB即为黄金三角形，黄金三角形的定义为：满足≈0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：______；
    （2）如图1，设AB=1，请你说明为什么k约为0.618；
    （3）由线段的黄金分割点联想到图形的“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分（设S1＜S2），如果，那么称直线l为该图形的黄金分割线．（如图3），点P是线段AB的黄金分割点，那么直线CP是△ABC的黄金分割线吗？请说明理由；
    （4）图3中的△ABC的黄金分割线有几条？

    查看答案和解析>>

    同步练习册答案