
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,-2).
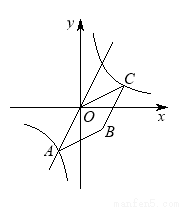
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移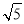 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
(1)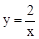 ;(2)为﹣1<x<0或x>1 ;(3)四边形OABC是菱形.
;(2)为﹣1<x<0或x>1 ;(3)四边形OABC是菱形.
【解析】
试题分析:(1)设反比例函数的解析式为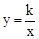 (k>0),先利用y=2x求出点A的坐标,然后代入即可;
(k>0),先利用y=2x求出点A的坐标,然后代入即可;
(2)根据函数图像解答即可;(3)观察图形猜想:四边形OABC是菱形,先证明四边形OABC是平行四边形,然后再证明OC=OA即可.
试题解析:
【解析】
(1)设反比例函数的解析式为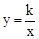 (k>0)
(k>0)
∵A(m,﹣2)在y=2x上
∴﹣2=2m
∴m=﹣1
∴A(﹣1,﹣2)
又∵点A在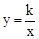 上
上
∴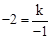
∴k=2,∴反比例函数的解析式为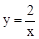 3分
3分
(2)由图知:正比例函数值大于反比例函数值时自变量x的取值范围为﹣1<x<0或x>1 5分
(3)四边形OABC是菱形.证明如下:
∵A(﹣1,﹣2)∴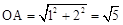
由题意知:CB∥OA且CB=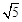 ,∴CB=OA
,∴CB=OA
∴四边形OABC是平行四边形 7分
∵C(2,n)在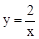 上,∴
上,∴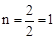 ,∴C(2,1),∴
,∴C(2,1),∴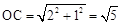 ,∴OC=OA
,∴OC=OA
∴平行四边形OABC是菱形。 10分
考点:1.反比例函数;2.函数图像与不等式;3.菱形的判定.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分) 如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形AB-CD的边AB上的“强相似点”,解决问题:
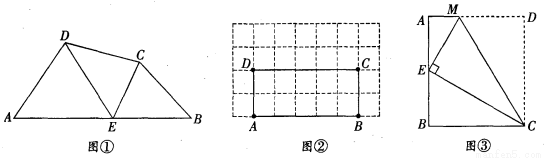
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由:
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:选择题
若关于x的方程x2-2(1- k)x+k2=0有实数根m和n,则m+n的取值范围是( )
A.m+n≥1 B.m+n≤1
C.m+n≥ D.m+n≤
D.m+n≤
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:填空题
如图,等腰直角三角形ABC的顶点A,C在x轴上,∠ACB=90°,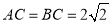 ,反比例
,反比例
函数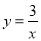 (
(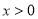 )的图象分别与AB,BC交于点D,E.连接DE,当△BDE∽△BCA时,点E的坐标为______________.
)的图象分别与AB,BC交于点D,E.连接DE,当△BDE∽△BCA时,点E的坐标为______________.
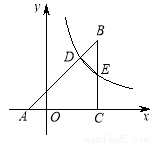
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:选择题
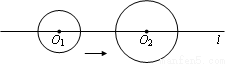
如图,圆O1、圆O2的圆心O1、O2在直线l上,圆O1的半径为2 cm,圆O2的半径为3 cm,O1O2=8 cm。圆O1以1 cm/s的速度沿直线l向右运动,7s后停止运动,在此过程中,圆O1与圆O2没有出现的位置关系是( )
A.外切 B.相交
C.内切 D.内含
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市毕业班正月联考数学试卷(解析版) 题型:填空题
如图,点A,B,C在⊙O上,若∠ABC=40°,则∠AOC的度数为 _________ .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市七年级上学期期中考试数学试卷(解析版) 题型:解答题
(13分)阅读下列材料并解决有关问题:
我们知道, 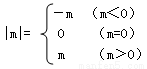 ,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|m+1|+|m-2|时,可令m+1=0和m-2=0,分别求得m=-1,m=2(称-1,2分别为|m+1|与|m-2|的零点值).在实数范围内,零点值m=-1和m=2可将全体实数分成不重复且不遗漏的如下3种情况:
,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|m+1|+|m-2|时,可令m+1=0和m-2=0,分别求得m=-1,m=2(称-1,2分别为|m+1|与|m-2|的零点值).在实数范围内,零点值m=-1和m=2可将全体实数分成不重复且不遗漏的如下3种情况:
(1)m<-1;(2)-1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m-2|可分以下3种情况:
(1)当m<-1时,原式=-(m+1)-(m-2)=-2m+1;
(2)当-1≤m<2时,原式=m+1-(m-2)=3;
(3)当m≥2时,原式=m+1+m-2=2m-1.
综上讨论,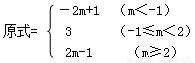
通过以上阅读,请你解决以下问题:
(1)分别求出|x-5|和|x-4|的零点值;
(2)化简代数式|x-5|+|x-4|.
(3) 求代数式|x-5|+|x-4|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com