
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
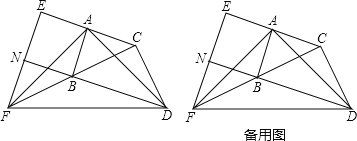
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
【答案】(1)详见解析;(2)详见解析;(3)四边形ABNE是正方形,理由详见解析.
【解析】
试题分析:(1)根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,求得∠ABF=135°,∠ABF=∠ACD,再证得BF=CD,由SAS证明△ABF≌△ACD,即可得出AD=AF;(2)由(1)知AF=AD,△ABF≌△ACD,得出∠FAB=∠DAC,证出∠EAF=∠BAD,由SAS证明△AEF≌△ABD,得出对应边相等即可;(3)由全等三角形的性质得出得出∠AEF=∠ABD=90°,证出四边形ABNE是矩形,由AE=AB,即可得出四边形ABNE是正方形.
试题解析:(1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABF=135°,
∵∠BCD=90°,
∴∠ABF=∠ACD,
∵CB=CD,CB=BF,∴BF=CD,
在△ABF和△ACD中,
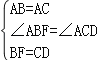 ,
,
∴△ABF≌△ACD(SAS),
∴AD=AF;
(2)证明:由(1)知,AF=AD,△ABF≌△ACD,
∴∠FAB=∠DAC,
∵∠BAC=90°,
∴∠EAB=∠BAC=90°,
∴∠EAF=∠BAD,
在△AEF和△ABD中,
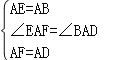 ,
,
∴△AEF≌△ABD(SAS),
∴BD=EF;
(3)解:四边形ABNE是正方形;理由如下:
∵CD=CB,∠BCD=90°,
∴∠CBD=45°,
由(2)知,∠EAB=90°,△AEF≌△ABD,
∴∠AEF=∠ABD=90°,
∴四边形ABNE是矩形,
又∵AE=AB,
∴四边形ABNE是正方形.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A.2a2-3ab+a=a(2a-3b)
B.2πR-2πr=π(2R-2r)
C.-x2-2x=-x(x-2)
D.5x4+25x2=5x2(x2+5)
查看答案和解析>>
科目:初中数学 来源: 题型:
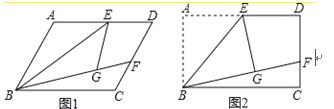
【题目】如图1,ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且 点G在□ABCD内部.将BG延长交DC于点F.
(1)猜想并填空:GF DF(填“>”、“<”、“=”);
(2)请证明你的猜想;
(3)如图2,当∠A=90°,设BG=a,GF=b,EG=c,证明:c2=ab.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东到学校参加毕业晚会演出,到学校时发现演出道具还放在家中,此时距毕业晚会开始还有25分钟,于是立即步行回家.同时,他父亲从家里出发骑自行车以他3倍的速度给他送道具,两人在途中相遇,相遇后,小东父亲立即骑自行车以原来的速度载小东返回学校.图中线段AB、OB表示相遇前(含相遇)父亲送道具、小东取道具过程中,各自离学校的路程S(米)与所用时间t分)之间的函数关系,结合图象解答下列问题.
(1)求点B坐标;
(2)求AB直线的解析式;
(3)小东能否在毕业晚会开始前到达学校?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.当A、B两点中有一点在原点时,不妨设点A在原点,
如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
当A、B两点都不在原点时,
如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;
①如图3,点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;
②如图4,点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= a +(-b)=∣a-b∣;

(2)回答下列问题:
①数轴上表示-3和-5的两点之间的距离是___ __
数轴上表示3和-3的两点之间的距离是___ ___;
②数轴上表示x和-3的两点A和B之间的距离是__ __,
如果∣AB∣=4,那么x为__ __;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com