
【题目】在△ABC中,点D、E分别在边AC、BC上(不与点A、B、C重合),点P是直线AB上的任意一点(不与点A、B重合).设∠PDA=x,∠PEB=y,∠DPE=m,∠C=n.
(1)如图,当点P在线段AB上运动,且n=90°时
①若PD∥BC,PE∥AC,则m=_____;
②若m=50°,求x+y的值.
(2)当点P在直线AB上运动时,直接写出x、y、m、n之间的数量关系.


【答案】(1)①90°,②140°;(2)详见解析.
【解析】分析:(1)①证明四边形DPEC为平行四边形可得结论;
②根据四边形内角和为360°,列等式求出x+y的值;
(2)根据P、D、E位置的不同,分五种情况:①y-x=m+n,如图2,点P在BA的延长线上时,根据三角形的内角和与外角定理列等式,化简后得出结论;
②x-y=m-n,如图3,点P在BA的延长线上时,根据三角形的内角和与外角定理列等式,化简后得出结论;
③x+y=m+n,如图4,点P在线段BA上时,根据四边形的内角和为360°列等式,化简后得出结论;
④x-y=m+n,如图5,同理得出结论;
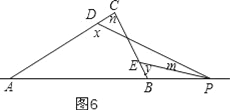
⑤y-x=m-n,如图6,同理得出结论.
详解:(1)①如图1,
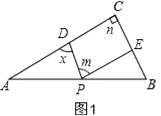
∵PD∥BC,PE∥AC,
∴四边形DPEC为平行四边形,
∴∠DPE=∠C,
∵∠DPE=m,∠C=n=90°,
∴m=90°;
②∵∠ADP=x,∠PEB=y,
∴∠CDP=180°-x,∠CEP=180°-y,
∵∠C+∠CDP+∠DPE+∠CEP=360°,
∠C=90°,∠DPE=50°,
∴90°+180°-x+50°+180°-y=360°,
∴x+y=140°;
(2)分五种情况:
①y﹣x=m+n,如图2,
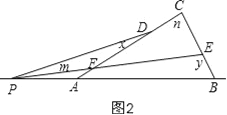
理由是:
∵∠DFP=n+∠FEC,∠FEC=180°﹣y,
∴∠DFP=n+180°﹣y,
∵x+m+∠DFP=180°,
∴x+m+n+180°﹣y=180°,
∴y﹣x=m+n;
②x﹣y=m﹣n,如图3,
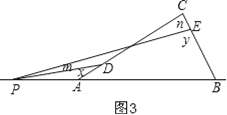
理由是:
同理得:m+180°﹣x=n+180°﹣y,
∴x﹣y=m﹣n;
③x+y=m+n,如图4,

理由是:
由四边形内角和为360°得:180°﹣x+m+180°﹣y+n=360°,
∴x+y=m+n;
④x﹣y=m+n,如图5,
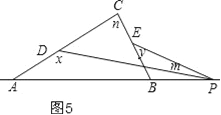
理由是:
同理得:180°=m+n+y+180°﹣x,
∴x﹣y=m+n;
⑤y﹣x=m﹣n,如图6,
理由是:
同理得:n+180°﹣x=m+180°﹣y,
∴y﹣x=m﹣n.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论: ①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )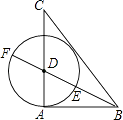
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )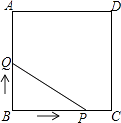
A.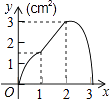
B.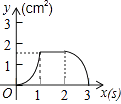
C.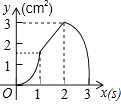
D.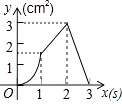
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
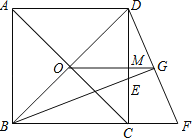
(1)求证:△BCE≌△DCF.
(2)判断OG与BF有什么关系,证明你的结论.
(3)若DF2=8-4![]() ,求正方形ABCD的面积?
,求正方形ABCD的面积?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com