
如图,抛物线 (b,c是常数,且c<0)与
(b,c是常数,且c<0)与 轴分别交于点A、B(点A位于点B的左侧),与
轴分别交于点A、B(点A位于点B的左侧),与 轴的负半轴交于点C,点A的坐标为(-1,0).
轴的负半轴交于点C,点A的坐标为(-1,0).
(1)请直接写出点OA的长度;
(2)若常数b,c满足关系式: .求抛物线的解析式.
.求抛物线的解析式.
(3)在(2)的条件下,点P是 轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.
轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有多少个(直接写出结果)?
(1)OA=1;(2)抛物线的解析式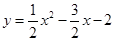 ;(3)①0<S<5;②
;(3)①0<S<5;②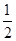 +c,﹣2c;11.
+c,﹣2c;11.
解析试题分析:(1)由点A的坐标为(-1,0)可得:OA=1;
(2)根据抛物线 过点A (-1,0),得到:b = c+
过点A (-1,0),得到:b = c+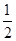 ,联立
,联立 ,求出b,c的值即可;
,求出b,c的值即可;
(3)①分两种情况进行讨论:(Ⅰ)当﹣1<x<0时;(Ⅱ)当0<x<4时;
②由0<S<5,S为整数,得出S=1,2,3,4.分两种情况进行讨论:(Ⅰ)当﹣1<x<0时,(Ⅱ)当0<x<4时.
试题解析:(1)OA=1;
(2)∵抛物线 过点A (-1,0),
过点A (-1,0),
∴b=c+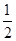 ,
,
∵ ,
,
∴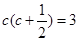 ,
,
∵c<0,
∴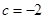 ,
,
∴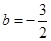 ,
,
∴抛物线的解析式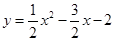 ;
;
(3)①设点P坐标为(x,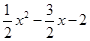 ).
).
∵点A的坐标为(﹣1,0),点B坐标为(4,0),点C坐标为(0,﹣2),
∴AB=5,OC=2,直线BC的解析式为y=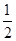 x﹣2.
x﹣2.
分两种情况:
(Ⅰ)当﹣1<x<0时,0<S<S△ACB.
∵S△ACB=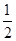 AB•OC=5,
AB•OC=5,
∴0<S<5;
(Ⅱ)当0<x<4时,过点P作PG⊥x轴于点G,交CB于点F.
∴点F坐标为(x,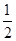 x﹣2),
x﹣2),
∴PF=PG﹣GF=﹣(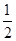 x2﹣
x2﹣ x﹣2)+(
x﹣2)+(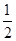 x﹣2)=﹣
x﹣2)=﹣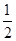 x2+2x,
x2+2x,
∴S=S△PFC+S△PFB=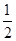 PF•OB=
PF•OB=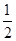 (﹣
(﹣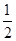 x2+2x)×4=﹣x2+4x=﹣(x﹣2)2+4,
x2+2x)×4=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,S最大值=4,
∴0<S≤4.
综上可知0<S<5;
②∵0<S<5,S为整数,
∴S=1,2,3,4.
分两种情况:
(Ⅰ)当﹣1<x<0时,设△PBC中BC边上的高为h.
∵点A的坐标为(﹣1,0),点B坐标为(4,0),点C坐标为(0,﹣2),
∴AC2=1+4=5,BC2=16+4=20,AB2=25,
∴AC2+BC2=AB2,∠ACB=90°,BC边上的高AC=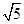 .
.
∵S=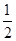 BC•h,∴h=
BC•h,∴h=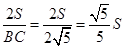 .
.
如果S=1,那么h=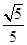 ×1=
×1=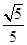 <
<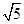 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;
如果S=2,那么h=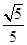 ×2=
×2=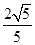 <
<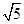 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;
如果S=3,那么h=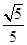 ×3=
×3=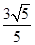 <
<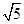 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;
如果S=4,那么h=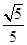 ×4=
×4=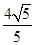 <
<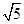 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;
即当﹣1<x<0时,满足条件的△PBC共有4个;
(Ⅱ)当0<x<4时,S=﹣x2+4x.
如果S=1,那么﹣x2+4x=1,即x2﹣4x+1=0,
∵△=16﹣4=12>0,∴方程有两个不相等的实数根,此时P点有2个,△PBC有2个;
如果S=2,那么﹣x2+4x=2,即x2﹣4x+2=0,
∵△=16﹣8=8>0,∴方程有两个不相等的实数根,此时P点有2个,△PBC有2个;
如果S=3,那么﹣x2+4x=3,即x2﹣4x+3=0,
∵△=16﹣12=4>0,∴方程有两个不相等的实数根,此时P点有2个,△PBC有2个;
如果S=4,那么﹣x2+4x=4,即x2﹣4x+4=0,
∵△=16﹣16=0,∴方程有两个相等的实数根,此时P点有1个,△PBC有1个;
即当0<x<4时,满足条件的△PBC共有7个;
综上可知,满足条件的△PBC共有4+7=11个.
故答案为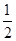 +c,﹣2c;11.
+c,﹣2c;11.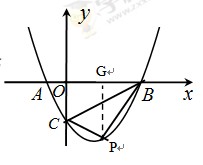 .
.
考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,已知点 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与 轴相交于点
轴相交于点 ,连结
,连结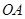 ,抛物线y=x
,抛物线y=x
 从点
从点 沿
沿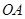 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点 ,顶点
,顶点 到
到 点时停止移动.
点时停止移动.
(1)求线段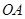 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点 的横坐标为
的横坐标为 ,
,
①用 的代数式表示点
的代数式表示点 的坐标;
的坐标;
②当 为何值时,线段
为何值时,线段 最短;
最短;
(3)当线段 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点 ,使△
,使△ 的面积与△
的面积与△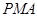 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
宁波元康水果市场某批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价一元,日销售量将减少20千克.
(1)现要保证每天盈利6000元,同时又要让顾客得到实惠,那么每千克应涨价多少元?
(2)若该批发商单纯从经济角度看,那么每千克应涨价多少元,能使商场获利最多.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:红星建材店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该建材店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该建材店要获得最大月利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,抛物线经过A(-1,0),B(4,0),C(0,-4),⊙M是△ABC的外接圆,M为圆心。
⑴求抛物线的解析式;
⑵求阴影部分的面积;
⑶在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=K,△CPQ的面积为S,求S关于K的函数关系式,并求出S的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为ts,四边形APQC的面积为ycm2.
(1)当t为何值时,△PBQ是直角三角形?
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为xcm,试求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数图像与y轴交于点(0,-4),并经过(-1,-6)和(1,2)
(1)求这个二次函数的解析式;
(2)求出这个函数的图像的开口方向,对称轴和顶点坐标;
(3)该函数图像与x轴的交点坐标 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com