
已知二次函数图像与y轴交于点(0,-4),并经过(-1,-6)和(1,2)
(1)求这个二次函数的解析式;
(2)求出这个函数的图像的开口方向,对称轴和顶点坐标;
(3)该函数图像与x轴的交点坐标 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
如图,抛物线 (b,c是常数,且c<0)与
(b,c是常数,且c<0)与 轴分别交于点A、B(点A位于点B的左侧),与
轴分别交于点A、B(点A位于点B的左侧),与 轴的负半轴交于点C,点A的坐标为(-1,0).
轴的负半轴交于点C,点A的坐标为(-1,0).
(1)请直接写出点OA的长度;
(2)若常数b,c满足关系式: .求抛物线的解析式.
.求抛物线的解析式.
(3)在(2)的条件下,点P是 轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.
轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有多少个(直接写出结果)?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知关于x的方程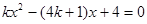 .
.
(1)当k取何值时,方程有两个实数根;
(2)若二次函数 的图象与
的图象与 轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
(3)若(2)中的抛物线与x轴交于A、B两点,与y轴交于C点.将抛物线向上平移n个单位,使平移后得到的抛物线的顶点落在△ABC的内部(不包括△ABC的边界),写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
天猫商城旗舰店销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设该旗舰店每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果旗舰店想要每月获得的利润不低于2000元,那么每月的成本最少需要 元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资,已知生产每件产品的成本是40元.在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额一生产成本—投资)为z(万元).
(1)试写出y与x之间的函数关系式(不写x的取值范围);
(2)试写出z与x之间的函数关系式(不写x的取值范围);
(3)公司计划,在第一年按年获利最大确定销售单价进行销售;到第二年年底获利不低于1130万元,请借助函数的大致图象说明:第二年的销售单价x(元)应确定在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:关于 的二次函数y=px2-(3p+2)x+2p+2(p>0)
的二次函数y=px2-(3p+2)x+2p+2(p>0)
(1)求证:无论p为何值时,此函数图象与x轴总有两个交点;
(2)设这两个交点坐标分别为(x1,0),(x2,0)(其中x1<x2)且S=x2-2x1,求S关于P的函数解析式
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com