
【题目】解答
(1)观察与归纳:在如图1所示的平面直角坐标系中,直线l与y轴平行,点A与点B是直线l上的两点(点A在点B的上方).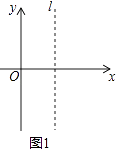
①小明发现:若点A坐标为(2,3),点B坐标为(2,﹣4),则AB的长度为;
②小明经过多次取l上的两点后,他归纳出这样的结论:若点A坐标为(t,m),点B坐标为(t,n),当m>n时,AB的长度可表示为;
(2)如图2,正比例函数y=x与一次函数y=﹣x+6交于点A,点B是y=﹣x+6图象与x轴的交点,点C在第四象限,且OC=5.点P是线段OB上的一个动点(点P不与点O,B重合),过点P与y轴平行的直线l交线段AB于点Q,交射线OC于R,设点P横坐标为t,线段QR的长度为m.已知当t=4时,直线l恰好经过点C.
①求点A的坐标;
②求OC所在直线的关系式;
③求m关于t的函数关系式.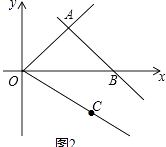
【答案】
(1)7;m﹣n
(2)
解:①解 ![]() 得
得 ![]() ,
,
∴A(3,3);
②∵直线l平行于y轴且当t=4时,直线l恰好过点C,如图2,作CE⊥OB于E,
∴OE=4,
在Rt△OCE中,OC=5,
由勾股定理得:
CE= ![]() =3,
=3,
∴点C的坐标为:(4,﹣3);
设OC所在直线的关系式为y=kx,则﹣3=4k,
∴k=﹣ ![]() ,
,
∴OC所在直线的关系式为y=﹣ ![]() x;
x;
③由直线y=﹣x+6可知B(6,0),
作AD⊥OB于D,
∵A(3,3),
∴OD=BD=AD=3,
∴∠AOB=45°,OA=AB,
∴∠OAB=90°,∠ABO=45°
当0<t≤3时,如图2,
∵直线l平行于y轴,
∴∠OPQ=90°,
∴∠OQP=45°,
∴OP=QP,
∵点P的横坐标为t,
∴OP=QP=t,
在Rt△OCE中,
∵tan∠EOC=|k|= ![]() ,
,
∴tan∠POR= ![]() =
= ![]() ,
,
∴PR=OPtan∠POR= ![]() t,
t,
∴QR=QP+PR=t+ ![]() t=
t= ![]() t,
t,
∴m关于t的函数关系式为:m= ![]() t;
t;
当3<t<6时,如图3,
∵∠BPQ=90°,∠ABO=45°,
∴∠BQP=∠PBQ=45°,
∴BP=QP,
∵点P的横坐标为t,
∴PB=QP=6﹣t,
∵PR∥CE,
∴△BPR∽△BEC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:PR=9﹣ ![]() t,
t,
∴QR=QP+PR=6﹣t+9﹣ ![]() t=15﹣
t=15﹣ ![]() t,
t,
∴m关于t的函数关系式为:m=15﹣ ![]() t;
t;
综上,m关于t的函数关系式为m= 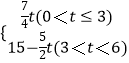
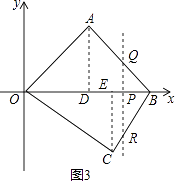

【解析】解:(1)①若点A坐标为(2,3),点B坐标为(2,﹣4),则AB的长度为3﹣(﹣4)=7;②若点A坐标为(t,m),点B坐标为(t,n),当m>n时,AB的长度可表示为m﹣n;
所以答案是7;m﹣n;
【考点精析】通过灵活运用正比例函数的图象和性质和一次函数的图象和性质,掌握正比函数图直线,经过一定过原点.K正一三负二四,变化趋势记心间.K正左低右边高,同大同小向爬山.K负左高右边低,一大另小下山峦;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:

已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(2)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(2)中的最大利润少了2250元.请问本次成套的销售量为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据有关部门统计,2019年春节期间,广东各大景点的游客总数约25200000人次,将数25200000用科学记数法表示为( )
A.2.52×107B.2.52×108C.0.252×107D.0.252×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于 ![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 . 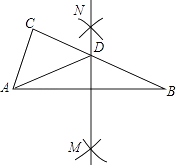
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com