
����Ŀ��Ϊ�˽�ij�������꼶ѧ�������š����������������֡�Ϸ��������ӽ�Ŀ��ϲ��������Ӹõ��������ȡ�������꼶ѧ����Ϊ�����������ʾ�����ķ����ռ����ݣ������ʾ������ÿ��ͬѧֻ��ѡ������һ���Ŀ����������õ�������������ı�������ͼ����ʾ������ͼ��û������ɣ�
��Ŀ���� | ���� | ���� | ���� | ���� | Ϸ�� |
���� | 36 | 90 | a | b | 27 |
���ݱ���ͼ�ṩ����Ϣ������������⣺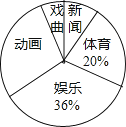
��1�����������a��b��ֵ��
��2��������ͳ��ͼ�б�ʾ����������������Ӧ�����ε�Բ�ĽǶ�����
��3�����õ������꼶ѧ������47500�ˣ��Թ��Ƹõ������꼶ѧ����ϲ�������š�����ӽ�Ŀ��ѧ���ж����ˣ�
���𰸡�
��1��
�⣺��ϲ��������������90�ˣ�ռ��������20%��
��������= ![]() =450���ˣ���
=450���ˣ���
����������ռ36%��
��a=450��36%=162���ˣ���
��b=450��162��36��90��27=135���ˣ���
��2��
�⣺��ϲ��������������135�ˣ�
�� ![]() ��360��=108��
��360��=108��
��3��
�⣺��ϲ�������������İٷֱ�= ![]() ��100%=8%��
��100%=8%��
��47500��8%=3800���ˣ���
�𣺸õ������꼶ѧ����ϲ�������š�����ӽ�Ŀ��ѧ����3800��
����������1���������ȡ���������������b��ֵ�������ɵó�a��ֵ��
����������2�����a��ֵ���������ıȿɵó����ۣ�
����������3�����ϲ�������������İٷֱȣ������ɵó����ۣ����⿼���������ͳ��ͼ����֪ͨ������ͳ��ͼ���Ժ�����ر�ʾ������������ͬ����֮��Ĺ�ϵ��������Բ�������ʾ��������λ1������Բ�����������ʾ������ռ�����İٷ����ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨��logab��a��0��a��1��b��0����ʾa��b֮���һ�����㣮
�������µ����㷨��lognan=n��logNM= ![]() ��a��0��a��1��N��0��N��1��M��0����
��a��0��a��1��N��0��N��1��M��0����
���磺log223=3��log25= ![]() ����log1001000=
����log1001000=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ʵ�Ա��Ħ�г����ʾֳ�������������2km����A�壬����������3km����B�壬Ȼ����������9km��C�壬���ص��ʾ֣�
��1�����ʾ�Ϊԭ�㣬������Ϊ��������1����λ���ȱ�ʾ1km�������������ϱ�ʾ��A��B��C������ׯ��λ�ã�
![]()
��2��C����A���ж�Զ��
��3����Ħ�г�ÿ1km����0.03��������·�����Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�κ���y=kx+2k-3(k��0),������������k��ֵk1,k2,�ֱ��Ӧ����һ�κ���ֵy1,y2,��k1k2<0,��x=mʱ,ȡ��Ӧy1,y2,�еĽ�Сֵp,��p�����ֵ��________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲���������

����������ӳ�Ĺ��ɣ������6�����6�еĽ�����ϵ���ӦΪ������
��1����n�����n�еĽ�����ϵ���ӦΪ���٣����ú�������n��ʽ�ӱ�ʾ��
��2���������Ͻ�2��2������������������֮�ͣ�����![]()
![]() ����������ȡ����2��2�������Σ�����������������֮�ͣ�������ó��Ľ��ۣ�
����������ȡ����2��2�������Σ�����������������֮�ͣ�������ó��Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��k��0���뷴��������y= ![]() ��ͼ���ཻ��A��B���㣬һ�κ�����ͼ����y���ཻ�ڵ�C����֪��A��4��1��
��ͼ���ཻ��A��B���㣬һ�κ�����ͼ����y���ཻ�ڵ�C����֪��A��4��1�� 
��1�����������Ľ���ʽ��
��2������OB��O������ԭ�㣩������BOC�����Ϊ3�����һ�κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��һ���̻���������Ӱ������Ϊ���ԣ���֪AB=15��AC=9��BC=12����Ӱ�����ǡ�ABC������Բ��һֻ���ɷ����С�������������̻����ϣ���С�����ڻ����ϵĸ���Ϊ�������� 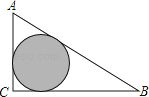
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�е���̨����Ϊ�˽������ȡ���ŵ���Ҫͼ����ͨ������������Ƶ�һ������ͳ��ͼ��������Լ��230���ˣ���ɹ������н���ֽ���ֻ�������Ϊ��ȡ���ŵ���Ҫ;������������ԼΪ���ˣ�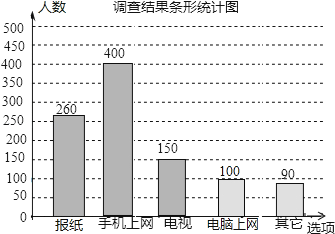
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6�֣�������С�������һ����
��Ŀ����ͬһƽ���ϣ�����BOA=70������BOC=15������AOC�Ķ�����
�⣺��������ɻ���ͼ��

�ߡ�AOC=��BOA����BOC
=70����15��
=55����
���AOC=55����
��������ʦ������С�������������ᣬ˵�����ɣ������ᣬ�뽫С�����ĵĴ���ָ��������������Ϊ��ȷ�Ľⷨ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com