
(本题10分)在Rt△ABC中,∠CAB=90°,AB=AC.
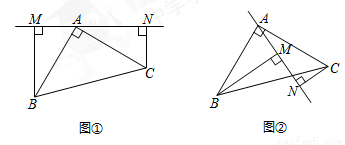
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.
①判断线段MN、BM、CN之间有何数量关系,并证明;
②若AM=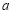 ,BM=
,BM= ,AB=
,AB= ,试利用图①验证勾股定理
,试利用图①验证勾股定理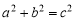 ;
;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)
(1)①MN=BM+CN,理由见试题解析;②证明见试题解析;(2)MN=BM﹣CN.
【解析】
试题分析:(1)①利用已知得出∠MAB=∠ACN,进而得出△MAB≌△NCA,进而得出BM=AN,AM=CN,即可得出线段MN、BM、CN之间的数量关系;
②利用S梯形MBCN=S△MAB+S△ABC+S△NCA,S梯形MBCN=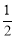 (BM+CN)×MN=
(BM+CN)×MN=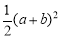 ,进而得出答案;
,进而得出答案;
(2)利用已知得出∠MAB=∠ACN,进而得出△MAB≌△NCA,进而得出BM=AN,AM=CN,即可得出线段MN、BM、CN之间的数量关系.
试题解析:(1)①MN=BM+CN;
理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,∴∠MAB=∠ACN,
在△MAB和△NCA中,∵∠BMA=∠ANC,∠MAB=∠NCA,AB=AC,∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,∴MN=AM+AN=BM+CN;
②由①知△MAB≌△NCA,∴CN=AM=a,AN=BM=b,AC=BC=c,∴MN=a+b,
∵S梯形MBCN=S△MAB+S△ABC+S△NCA=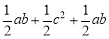 ,S梯形MBCN=
,S梯形MBCN=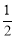 (BM+CN)×MN=
(BM+CN)×MN=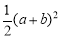 ,
,
∴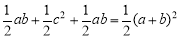 ,∴
,∴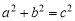 ;
;
(2)MN=BM﹣CN;
理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,∴∠MAB=∠ACN,
在△MAB和△NCA中,∵∠BMA=∠ANC,∠MAB=∠NCA,AB=AC,∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,∴MN=AN﹣AM=BM﹣CN.
考点:全等三角形的判定与性质.


科目:初中数学 来源:2014-2015学年江苏省兴华顾庄等三校九年级上学期期中考试数学试卷(解析版) 题型:解答题
当自变量x =4时,二次函数有最小值 3,且它的图像与x轴的一个交点的横坐标为1.求这个二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校八年级上学期期中联考数学试卷(解析版) 题型:选择题
在平面直角坐标系中,点A(-2, 3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校七年级上学期期中联考数学试卷(解析版) 题型:选择题
将数据36 000 000用科学记数法表示是
A.3.6×107 B.0.36×108 C.36×107 D.3.6×106
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省丹阳市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题7分)如图,在长度为1个单位长度的正方形网格中,点A、B、C在小正方形的顶点上.

(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′;则点B′、 C′的坐标分别为( 、 ) ( 、 )
(2)在直线l上找一点P(在答题纸上图中标出),使PB+PC的长最短,这个最短长度的平方值是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(10分)某校学生会向全校1900名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
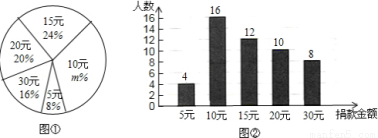
(1)本次接受随机抽样调查的学生人数为________ ,图①中m的值是________;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com