
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论.
(2)已知AB=1,∠ABE=45°,求BC的长.

【答案】(1)见解析;(2) .
.
【解析】(1)由矩形的性质和角平分线的定义得出∠DEC=∠ECB=∠BEC,推出BE=BC即可;
(2)求出AE=AB=1,根据勾股定理求出BE即可.
详解:(1) △BEC为等腰三角形
∵矩形ABCD,∴AD∥BC,
∴

又∵


∴△BEC为等腰三角形.
(2)∵矩形ABCD,
∴ .
.
又∵AB=1,∠ABE=45°∴由勾股定理得
 ,
,
由(1)得 .
.
点睛:本题考查了矩形的性质,等腰三角形的判定,勾股定理的应用,主要考察学生的推理能力,题目比较好,难度适中.
【题型】解答题
【结束】
23
某市为了构建城市立体道路网络,决定修建一条轻轨铁路,为使工程提前半年完成,需要将工作效率提高25%,原计划完成这项工程需要多少个月?
科目:初中数学 来源:北京市2017-2018学年七年级下学期期末数学试卷 题型:解答题
化简求值:(1)先化简再求值:(a-2)2+(2a-1)(a+4),其中a=-2.
(2)先化简,再求值:(2a+b)(2a-b)+b(2a+b)-4a2,其中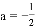 ,b=2.
,b=2.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级下学期期末数学试卷 题型:单选题
如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )

A. 40° B. 50° C. 60° D. 140°
查看答案和解析>>
科目:初中数学 来源:2018年秋冀教版九年级数学上册同步练习:28.2 过三点的圆 题型:填空题
如图,点 ,
, ,
, 均在
均在 的正方形网格格点上,过
的正方形网格格点上,过 ,
, ,
, 三点的外接圆除经过
三点的外接圆除经过 ,
, ,
, 三点外还能经过的格点数为 .
三点外还能经过的格点数为 .

查看答案和解析>>
科目:初中数学 来源:2018年秋冀教版九年级数学上册同步练习:28.2 过三点的圆 题型:单选题
在同一平面内,过已知A,B,C三个点可以作的圆的个数为( )
A. 0 B. 1 C. 2 D. 0或1
查看答案和解析>>
科目:初中数学 来源:2018年秋冀教版九年级数学上册同步测试:28.1~28.4 题型:单选题
如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
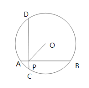
A.3 B.4
C.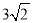 D.
D.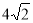
查看答案和解析>>
科目:初中数学 来源:2018年秋冀教版九年级数学上册第二十八章 圆练习题 题型:解答题
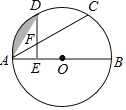
如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com