
【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
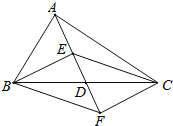
①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
科目:初中数学 来源: 题型:
【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁,图中折线O﹣A﹣B﹣C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
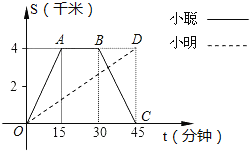
(1)小聪在天一阁查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知当x=1时,代数式ax3+bx+1的值为2018,则当x=-1时,代数式ax3+bx+1的值为( )
A. -2016 B. -2017 C. -2018 D. 2016
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路匀速驶向C城.已知A、C两城的距离为360km,B、C两城的距离为320km,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为xkm/h.
(1)根据题意填写下表:
行驶的路程(km) | 速度(km/h) | 所需时间(h) | |
甲车 | 360 |
|
|
乙车 | 320 | x |
|
(2)求甲、乙两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知抛物线y=k(x+1)(x﹣3k)(且k>0)与x轴分别交于A、B两点,A点在B点左边,与Y轴交于C点,连接BC,过A点作AE∥CB交抛物线于E点,0为坐标原点.
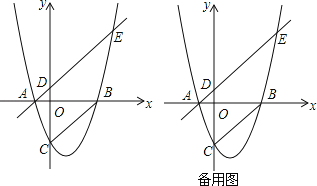
(1)用k表示点C的坐标(0, );
(2)若k=1,连接BE,
①求出点E的坐标;
②在x轴上找点P,使以P、B、C为顶点的三角形与△ABE相似,求出P点坐标;
(3)若在直线AE上存在唯一的一点Q,连接OQ、BQ,使OQ⊥BQ,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com