
����Ŀ����ͼ��������AOB�У�OA��OB�ǰ뾶����OA��4����AOB��120������P�ǻ�AB�ϵ�һ�����㣬����AP��BP���ֱ���OC��PA��OD��PB������ֱ�ΪC��D������CD��
��1����ͼ�٣��ڵ�P���ƶ������У��߶�CD�ij��Ƿ�ᷢ���仯�����������仯��������߶�CD�ij������ᷢ���仯����˵�����ɣ�
��2����ͼ�ڣ�����M��NΪ![]() �����ȷֵ㣬��IΪ��DOC�����ģ�����P�ӵ�M�˶���N��ʱ����I��������·����Ϊ__________����ֱ��д�������
�����ȷֵ㣬��IΪ��DOC�����ģ�����P�ӵ�M�˶���N��ʱ����I��������·����Ϊ__________����ֱ��д�������

���𰸡���1��![]() ����2��
����2��![]() ��
��
���������������:(1)������AB,��ΪCD����PAB����λ��,����CD=![]() ��ΪAB���Ȳ���,��CD���Ȳ���,����OA��4,��AOB��120��,���ý�ֱ�������εķ������AB,�ٸ�����λ�ߵ����ʼ������CD,
��ΪAB���Ȳ���,��CD���Ȳ���,����OA��4,��AOB��120��,���ý�ֱ�������εķ������AB,�ٸ�����λ�ߵ����ʼ������CD,
(2)��ΪCD����PAB����λ��,������λ�ߵ�����CD��AB,��Ϊ��I�ǡ�DOC������,���Ե�I��CD�Ĵ�ֱƽ������,Ȼ�������I�˶�·������OΪԲ��,OIΪ�뾶,Բ�Ľ�60�����ԵĻ���,���û�����ʽ���.
�������:��OA��OB,OH��AB,
��AH��BH��![]() AB,��AOH��
AB,��AOH��![]() ��AOB��60��,
��AOB��60��,
��Rt��AOH��,
�ߡ�OAH��30��,
��OH��![]() ��2,
��2,
����Rt��AOH,�ɹ��ɶ�����AH��![]() ��
��![]() ,
,
��AB��![]() ,
,
��CD��![]() ,
,
��2��![]() .
.


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��1��2����B��3��1����C����2����1����
��1����ͼ��������ABC����y��ԳƵ���A1B1C1��
��2��д��A1��B1��C1�����꣬A1�� ��B1��������C1����������ֱ��д���𰸣�
��3����A1B1C1�����Ϊ������ ����������ֱ��д���𰸣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��![]() ��y��
��y��![]() �ڵ�һ�����ڵ�ͼ����ͼ����P��y��
�ڵ�һ�����ڵ�ͼ����ͼ����P��y��![]() ��ͼ����һ���㣬PC��x���ڵ�C����y��
��ͼ����һ���㣬PC��x���ڵ�C����y��![]() ��ͼ���ڵ�B���������½��ۣ��١�ODB����OCA�������ȣ���PA��PBʼ����ȣ����ı���PAOB�������С���ᷢ���仯����CA��
��ͼ���ڵ�B���������½��ۣ��١�ODB����OCA�������ȣ���PA��PBʼ����ȣ����ı���PAOB�������С���ᷢ���仯����CA��![]() AP������������ȷ���۵�����ǣ�������
AP������������ȷ���۵�����ǣ�������
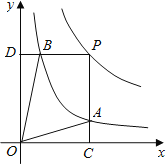
A. �٢ڢ� B. �ڢۢ� C. �٢ۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA��3��OC��5���ֱ���OA��OC����ֱ��Ϊx�ᡢy�ᣬ����ƽ��ֱ������ϵ��D�DZ�CB�ϵ�һ�����㣨����C��B�غϣ�������������y��![]() ��k��0����ͼ����D�����BA���ڵ�E������DE��
��k��0����ͼ����D�����BA���ڵ�E������DE��
��1������OE������EOA�����Ϊ3����k��___________��
��2���Ƿ���ڵ�D��ʹ�õ�B����DE�ĶԳƵ���OC�ϣ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
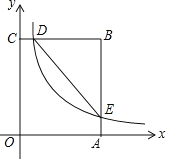
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪CD�Ǿ�����BCA����C��һ��ֱ�ߣ�CA=CB��E��F�ֱ���ֱ��CD�����㣬����BEC=��CFA=��![]() ��
��
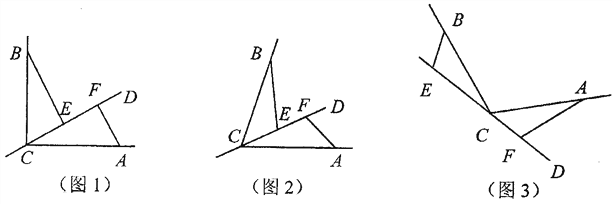
(1)��ֱ��CD������BCA���ڲ�����E��F������CD�ϣ������������⣺
����ͼ1����BCA=90������![]() =90����̽�������߶�EF��BE��AF��������ϵ��֤����Ľ���.
=90����̽�������߶�EF��BE��AF��������ϵ��֤����Ľ���.
����ͼ2����0������BCA��180���� ������һ��������![]() ����BCA��ϵ������___ ____ʹ���еĽ�����Ȼ������
����BCA��ϵ������___ ____ʹ���еĽ�����Ȼ������
(2)��ͼ3����ֱ��CD������BCA���ⲿ����![]() =��BCA����д�������߶�EF��BE��AF��������ϵ��֤����Ľ���.
=��BCA����д�������߶�EF��BE��AF��������ϵ��֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������߳���Ϊ2cm�������ΰ���ͼ��ʾ�ڷţ���A��B��C��D�ֱ����ĸ������ε����ģ���ͼ���Ŀ���Ӱ����ĺ�Ϊ�� ��

A��2cm2 B��4cm2 C��6cm2 D��8cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC������D�DZ�AB��һ�㣬EΪAC���е㣬����C��CF��AB�� ��DE���ӳ����ڵ�F��
��1����֤��DE=FE��
��2����CD=CF����A=40�㣬���BCD�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��AB��CD
��1����ͼ1����E��ֱ��BD����࣬�����ABE����CDE����BED��������ϵ����֤����Ľ��ۣ�
��2����ͼ2����E��ֱ��BD����࣬BF��DF�ֱ�ƽ�֡�ABE����CDE�������BFD�͡�BED��������ϵ����֤����Ľ��ۣ�
��3����ͼ3����E��ֱ��BD���Ҳ࣬BF��DF�ֱ�ƽ�֡�ABE����CDE����ô�ڣ�2�����С�BFD�͡�BED��������ϵ�IJ����Ƿ��Գ����������������֤�����������������д����IJ��룬��֤����

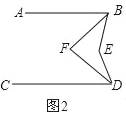

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪2��A�ͳ���1��B�ͳ���������һ�ο��˻�10��.��1��A�ͳ���2��B�ͳ���������һ�ο��˻�11��.ij������˾����31�ֻ���ƻ�ͬʱ����A�ͳ�a����B�ͳ�b��,һ�����꣬��ÿ���������ػ���.����������Ϣ����������⣺
��1��1��A�ͳ���1��B�ͳ���������һ�ηֱ���˻�����ٶ֣�
��2�������������˾��������
��3����A�ͳ�ÿ�������ÿ��100Ԫ��B�ͳ�ÿ�������ÿ��120Ԫ.��ѡ����ʡǮ�����������������ٵ����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com