
 如图所示,D是AB上一点,E是AC上一点.现给出以下三个条件:
如图所示,D是AB上一点,E是AC上一点.现给出以下三个条件:科目:初中数学 来源: 题型:
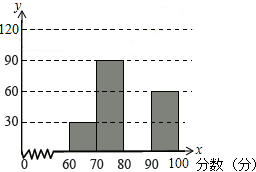 某校举行了一场学生“安全知识”问答竞赛活动,为了解笔试情况,随机抽查图表提供的信息,解答下列问题:
某校举行了一场学生“安全知识”问答竞赛活动,为了解笔试情况,随机抽查图表提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 10DF |
| CF |

查看答案和解析>>
科目:初中数学 来源: 题型:
 一圆形房间的地板上是由三个同心圆的图案所占满,它们的半径比为R1:R2:R3=1:
一圆形房间的地板上是由三个同心圆的图案所占满,它们的半径比为R1:R2:R3=1:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲种 | 乙种 | |
| 进价(元) | 4 | 5 |
| 售价(元) | a(6≥a>4) | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com