
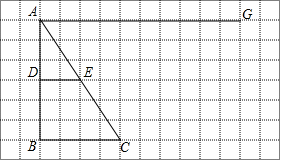
 如图,在网格图中,有△ABC与线段DE,在线段AG上是否存在点M,使得△MEC与△ADE相似?若存在,请先在图中确定出所有的点M,并选择其中一个说明理由;若不存在,也请说明理由.(图中各点均在格点上).
如图,在网格图中,有△ABC与线段DE,在线段AG上是否存在点M,使得△MEC与△ADE相似?若存在,请先在图中确定出所有的点M,并选择其中一个说明理由;若不存在,也请说明理由.(图中各点均在格点上). 分析 △ADE中,∠ADE=90°,DE是△ABC的中位线,则DE∥BC;如果过点E作EM⊥AC于M,则△AEM中有两个角与△ADE中的两个角分别对应相等,根据相似三角形的判定,可知两三角形相似.
解答 解:存在.
理由:过点E作AC的垂线,与AG交于一点M,点M即为所求.连接MC;
∵AD=DB,AE=EC,
∴DE是△ABC的中位线,
∴DE∥BC,AE=EC.
∵ME⊥AC,
∴△AEM≌△CEM.
∴∠MAE=∠MCE.
∵∠B=90°,
∴∠DAM=90°.
∵AF∥BC,
∴AM∥DE.
∴∠MAE=∠AED.
∴∠AED=∠MCE.
∵∠ADE=∠MEC=90°,
∴△MEC∽△ADE.
点评 本题主要考查相似三角形的判定、全等三角形的判定和性质、三角形的中位线定理等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,综合性较强,难度适中.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
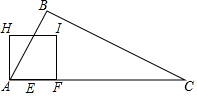 如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.
如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.88×105 | B. | 5.88×104 | C. | 58.8×103 | D. | 0.588×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,则△ABC的面积为42.
如图,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,则△ABC的面积为42.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com