
分析 方法一、由(a,b,c)和$(\frac{1}{a},\frac{1}{b},\frac{1}{c})$均为三角形数,得出a+b>c和$\frac{1}{b}+\frac{1}{c}>\frac{1}{a}$,联立两式,即可得$\frac{{3-\sqrt{5}}}{2}<\frac{a}{c}<\frac{{3+\sqrt{5}}}{2}$,再由a≤b≤c,得出$\frac{a}{c}≤1$,即可得出结论;
方法二、设$\frac{a}{c}=k$,同方法一即可得出结论.
解答 解:方法一、∵(a,b,c)为三角形数,
∴a+b>c.
∴b>c-a,
∴$\frac{1}{b}<\frac{1}{c-a}$,
∵$(\frac{1}{a},\frac{1}{b},\frac{1}{c})$为三角形数,
∴$\frac{1}{b}+\frac{1}{c}>\frac{1}{a}$,
∴$\frac{1}{a}<\frac{1}{b}+\frac{1}{c}<\frac{1}{c-a}+\frac{1}{c}$,
∴$\frac{1}{a}<\frac{1}{c-a}+\frac{1}{c}$,
两边同时乘以a(a>0),得,$1<\frac{a}{c-a}+\frac{a}{c}$,
即$\frac{c-a}{c}<\frac{a}{c-a}$,
化简得,a2-3ac+c2<0,
两边除以c2得,${({\frac{a}{c}})^2}-3(\frac{a}{c})+1<0$,
∴$\frac{{3-\sqrt{5}}}{2}<\frac{a}{c}<\frac{{3+\sqrt{5}}}{2}$
∵a≤b≤c,
∴$\frac{a}{c}≤1$,
∴$\frac{{3-\sqrt{5}}}{2}<\frac{a}{c}≤1$;
故答案为:$\frac{3-\sqrt{5}}{2}<\frac{c}{a}≤1$.
方法二、设$\frac{a}{c}=k$,
∵(a,b,c)为三角形数,
∴a+b>c,
∴b>c-a,
∴b>(1-k)c,
∴$\frac{1}{b}<\frac{1}{(1-k)c}$,
∵$(\frac{1}{a},\frac{1}{b},\frac{1}{c})$为三角形数,
∴$\frac{1}{b}+\frac{1}{c}>\frac{1}{a}$,
∴$\frac{1}{a}<\frac{1}{b}+\frac{1}{c}<\frac{1}{(1-k)c}+\frac{1}{c}$,
∴$\frac{1}{a}<\frac{1}{(1-k)c}+\frac{1}{c}$,
化简得,k2-3k+1<0,
解得$\frac{{3-\sqrt{5}}}{2}<k<\frac{{3+\sqrt{5}}}{2}$,
∵a≤b≤c,
∴k≤1,
∴$\frac{{3-\sqrt{5}}}{2}<k≤1$,
故答案为:$\frac{3-\sqrt{5}}{2}<\frac{c}{a}≤1$.
点评 此题是三角形边角关系,主要考查了新定义,三角形的两边之和第三边,解本题的关键是列出a+b>c和$\frac{1}{b}+\frac{1}{c}>\frac{1}{a}$两个不等式,对这两个式子的化简是解本题的难点.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
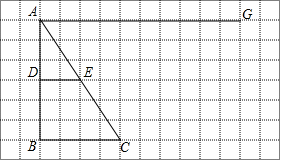 如图,在网格图中,有△ABC与线段DE,在线段AG上是否存在点M,使得△MEC与△ADE相似?若存在,请先在图中确定出所有的点M,并选择其中一个说明理由;若不存在,也请说明理由.(图中各点均在格点上).
如图,在网格图中,有△ABC与线段DE,在线段AG上是否存在点M,使得△MEC与△ADE相似?若存在,请先在图中确定出所有的点M,并选择其中一个说明理由;若不存在,也请说明理由.(图中各点均在格点上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
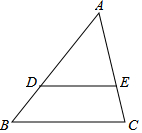 如图,画线段DE平行于BC,端点D,E分别在AB,AC上,再画线段FG平行于CA,HI平行于AB,端点也都分别在另两边上,在按上述要求画出的图形中,最少有5个三角形,最多有8个三角形.
如图,画线段DE平行于BC,端点D,E分别在AB,AC上,再画线段FG平行于CA,HI平行于AB,端点也都分别在另两边上,在按上述要求画出的图形中,最少有5个三角形,最多有8个三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 5 | 3 | 1 | m | -3 | … |
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )
一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )| A. | $\sqrt{73}$cm | B. | 3$\sqrt{6}$cm | C. | $\sqrt{61}$cm | D. | $\sqrt{53}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com