
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:选择题
 如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )
如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )| A. | x>1 | B. | 1<x<$\frac{5}{3}$ | C. | 1<x<2 | D. | 1<x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
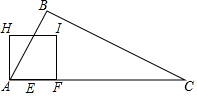 如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.
如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.88×105 | B. | 5.88×104 | C. | 58.8×103 | D. | 0.588×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
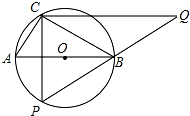 如图,Rt△ABC中,AB=10,AC:BC=3:4,以斜边AB为直径作⊙O,动点P在直径下方的半圆AB上运动(不与A、B重合),过点C作CQ⊥CP,与PB的延长线交于点Q.
如图,Rt△ABC中,AB=10,AC:BC=3:4,以斜边AB为直径作⊙O,动点P在直径下方的半圆AB上运动(不与A、B重合),过点C作CQ⊥CP,与PB的延长线交于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com