
分析 (1)直接利用算术平方根以及立方根的定义、绝对值的性质化简进而求出答案;
(2)直接利用平方差公式以及完全平方公式化简求出答案;
(3)直接化简二次根式,进而代入求出答案.
解答 解:(1)$\sqrt{16}$-$\root{3}{125}$+|$\sqrt{3}$-2|
=4-5+2-$\sqrt{3}$
=1-$\sqrt{3}$;
(2)($\sqrt{7}$+$\sqrt{3}$)($\sqrt{7}$-$\sqrt{3}$)-(2+$\sqrt{5}$)2
=7-3-(4+5+4$\sqrt{5}$)
=4-(9+4$\sqrt{5}$)
=-5-4$\sqrt{5}$;
(3)($\sqrt{a}$+$\sqrt{\frac{1}{b}}$)•$\sqrt{ab}$,
=a$\sqrt{b}$+$\sqrt{a}$
把a=8,b=6代入上式得:
原式=8$\sqrt{6}$+$\sqrt{8}$
=8$\sqrt{6}$+2$\sqrt{2}$.
点评 此题主要考查了二次根式的化简以及实数运算,正确化简二次根式是解题关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知y=-2x2+bx+c的图象经过点A(0,2)和B(-1,-4).
已知y=-2x2+bx+c的图象经过点A(0,2)和B(-1,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
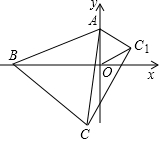 如图,在平面直角坐标系中,点A的坐标是(0,2),点B从坐标原点O出发,沿x轴负半轴运动,以AB为边作等边三角形ABC(A,B,C按逆时针顺序排列),当点B在原点O时,记此时的等边三角形为△AOC1.
如图,在平面直角坐标系中,点A的坐标是(0,2),点B从坐标原点O出发,沿x轴负半轴运动,以AB为边作等边三角形ABC(A,B,C按逆时针顺序排列),当点B在原点O时,记此时的等边三角形为△AOC1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E为BC的中点,若∠B=∠AEF=∠C=90°.连接AF
如图,点E为BC的中点,若∠B=∠AEF=∠C=90°.连接AF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
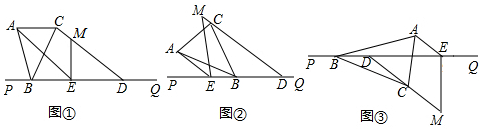
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com