
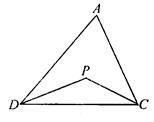

 ∠ADC,∠PCD=
∠ADC,∠PCD= ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解; ∠ADC,∠PCD=
∠ADC,∠PCD= ∠ACD,
∠ACD, ∠ADC-
∠ADC- ∠ACD,
∠ACD, (∠ADC+∠ACD),
(∠ADC+∠ACD), (180°-∠A),
(180°-∠A), ∠A;
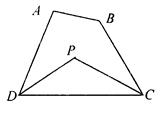
∠A; ∠ADC,∠PCD=
∠ADC,∠PCD= ∠BCD,
∠BCD, ∠ADC-
∠ADC- ∠BCD,
∠BCD, (∠ADC+∠BCD),
(∠ADC+∠BCD), (360°-∠A-∠B),
(360°-∠A-∠B), (∠A+∠B);
(∠A+∠B); ∠ADC,∠PCD=
∠ADC,∠PCD= ∠ACD,
∠ACD, ∠ADC-
∠ADC- ∠ACD,
∠ACD, (∠ADC+∠ACD),
(∠ADC+∠ACD), (720°-∠A-∠B-∠E-∠F),
(720°-∠A-∠B-∠E-∠F), (∠A+∠B+∠E+∠F)-180°,
(∠A+∠B+∠E+∠F)-180°, (∠A+∠B+∠E+∠F)-180°.
(∠A+∠B+∠E+∠F)-180°.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:不详 题型:解答题
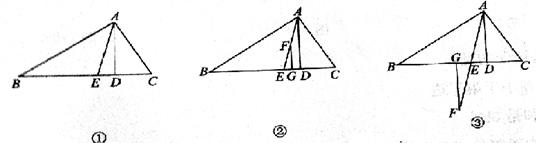
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
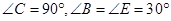 .
.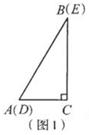
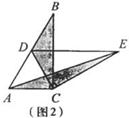
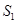 ,△AEC的面积为
,△AEC的面积为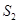 。则
。则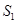 与
与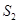 的数量关系是 。
的数量关系是 。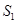 与
与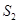 的数量关系仍然成立,并尝试分别作出了△BDC,△AEC中
的数量关系仍然成立,并尝试分别作出了△BDC,△AEC中 边上的高,请你证明小明的猜想。
边上的高,请你证明小明的猜想。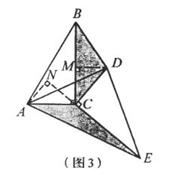
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com