
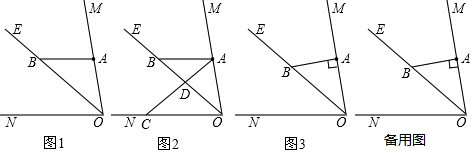
分析 (1)①如图1中,根据角平分线的定义以及平行线的性质即可解决问题;
②如图2中,根据∠OAC=∠BAO-∠BAD,想办法求出∠BAO,∠BAD即可;
(2)①当点D在线段OB上时,分三种情形讨论若∠ADB=∠ABD=55°;若∠BAD=∠ABD=55°,则∠OAD=90°-55°=35°,即x=35°,若∠ADB=∠BAD,则∠BAD=$\frac{1}{2}$(180°-∠ABD)=62.5°,推出∠OAD=90°-62.5°=27.5°,即x=27.5.
②当点D在射线BE上时,由∠ABD=180°-∠ABO=125°,推出∠DAB=∠ADB=27.5°,此时x=27.5+90=117.5则AD与ON不相交,所以舍弃,
解答 解:(1)①如图1中,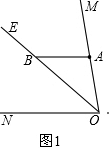
∵∠MON=70°,OB平分∠MON,
∴∠BON=$\frac{1}{2}$∠MON=35°,
∵AB∥ON,
∴∠ABO=∠BON=35°,
故答案为35°.
②如图2中,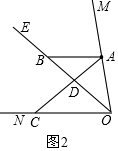
∵∠MON=70°,OE平分∠MON,
∴∠NOE=$\frac{1}{2}$∠MON=30°,
∵AB∥ON,
∴∠ABO=∠NOE=35°,∠BAO=180°-∠AON=110°,
∵∠BAD=∠ABD,∠ABD=35°,
∴∠BAD=35°,
∴∠OAC=∠BAO-∠BAD=110°-35°=75°,
∴x=75.
(2)如图3中,
∵∠AOB=35°,∠BAO=90°,
∴∠ABO=55°,
①当点D在线段OB上时,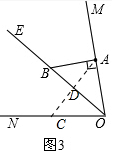
若∠ADB=∠ABD=55°,
∴∠BAD=180°-∠ADB-∠ABD=70°,
∴∠OAD=90°-70°=20°,即x=20,
若∠BAD=∠ABD=55°,则∠OAD=90°-55°=35°,即x=35°,
若∠ADB=∠BAD,则∠BAD=$\frac{1}{2}$(180°-∠ABD)=62.5°,
∴∠OAD=90°-62.5°=27.5°,即x=27.5.
②当点D在射线BE上时,∵∠ABD=180°-∠ABO=125°,
∴∠DAB=∠ADB=27.5°,
此时x=27.5+90=117.5则AD与ON不相交,所以舍弃,
综上所述,存在这样的x的值,使得△ADB中有两个相等的角,x的值为20或35或27.5.
点评 本题考查三角形综合题、角平分线的定义.平行线的性质、直角三角形的性质、时间最内角和定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论是思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
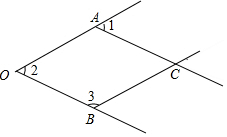 如图所示的是一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.(将下列解答过程补充完整)
如图所示的是一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.(将下列解答过程补充完整)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
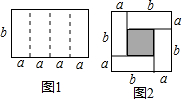 如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 3500 |
| 第二周 | 4台 | 10台 | 6000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com