
 如图,点A、B、C是⊙O上的三点,AB∥OC.
如图,点A、B、C是⊙O上的三点,AB∥OC.| 3 |
| 3 |
| AE |
| OC |
| PE |
| OP |
| 1 |
| 2 |
| PE | ||
|
| ||
| 3 |


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
| A、13,14 |
| B、14,13 |
| C、13,13 |
| D、13,13.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
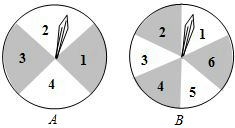 如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、5、6六个数字.有人为甲、乙两人设计了一个游戏,其规则如下:
如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、5、6六个数字.有人为甲、乙两人设计了一个游戏,其规则如下:查看答案和解析>>
科目:初中数学 来源: 题型:
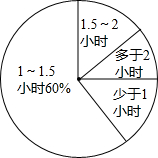 为进一步规范教育教学行为,切实减轻学生的课业负担,某校想了解本校九年级学生家庭作业用时情况.
为进一步规范教育教学行为,切实减轻学生的课业负担,某校想了解本校九年级学生家庭作业用时情况.| 家庭作业用时 | 频数(人数) | 频率 |
| 少于1小时 | 0.15 | |
| 1~1.5小时 | 60 | |
| 1.5~2小时 | 15 | b |
| 多于2小时 | ||
| 合计 | a | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
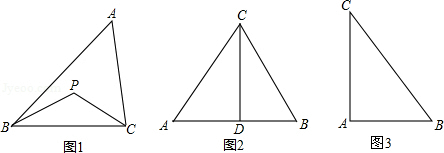
查看答案和解析>>
科目:初中数学 来源: 题型:
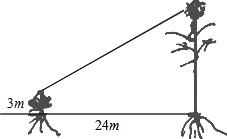 有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5.2m/s,那它至少需要多少时间才能赶回巢中?
有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5.2m/s,那它至少需要多少时间才能赶回巢中?查看答案和解析>>
科目:初中数学 来源: 题型:
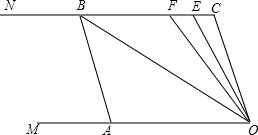 如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com