
在 中,AC=25,AB=35,
中,AC=25,AB=35, ,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
(1)如图1,当 时,求AE的长;
时,求AE的长;
(2)如图2,当点E、F在边AB上时,求
(3)联结CE,当 求
求 的值.
的值.
(1)AE=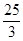 ;(2)
;(2)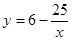 (
(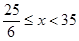 );(3)当△DEC和△ADF相似时
);(3)当△DEC和△ADF相似时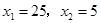 ,
,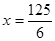
解析试题分析:
(1)先根据DF⊥AB,∠EDF=∠A,得出∠ADE=90°,再根据AD=5,tanA=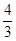 ,即可求出AE;
,即可求出AE;
(2)过点D作DG⊥AB,交AB于G,先证出△EDF∽△EAD,得出ED2=AE•EF,再求出DG、AG,最后根据EG=x-6,DE2=42+(x-3)2得出42+(x-3)2=x•(x-y),再进行整理即可;
(3)先证出∠AFD=∠EDC,再分两种情况讨论:①当∠A=∠CED时,得出AD:AC=AF:AE,5:25=y:x,再把y=6-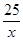 代入得出5(6-
代入得出5(6-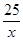 )=x,再解方程即可;
)=x,再解方程即可;
②当∠A=∠DCE时,根据△ECD∽△DAF得出CD:AF=CE:AD,20:y=x:5,再把y=6-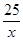 代入得出5(6-
代入得出5(6-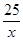 )=x,求出方程的解即可.
)=x,求出方程的解即可.
试题解析:
∵ ,
,
∴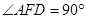 ,
,
∴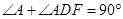
∵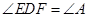 ,
,
∴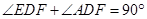 ,即
,即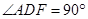
在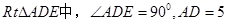 ,
,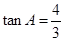
∴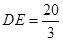
∴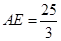
(2)过点 作
作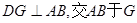
∵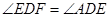 ,
,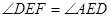
∴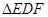 ∽
∽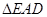
∴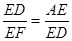
∴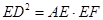
∴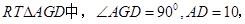
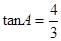
∴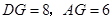 ∴
∴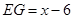 ∴
∴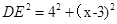
∴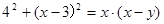
∴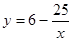 (
(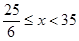 )
)
(3)∵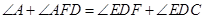 ,且
,且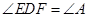 .
.
∴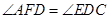
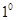 当
当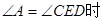
∵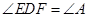 ,又∵
,又∵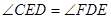 ∴
∴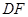 //
//
∴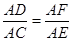 ∴
∴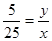 ∵
∵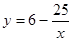 ∴
∴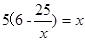
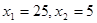
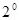 当
当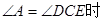
∵ ,∴
,∴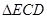 ∽
∽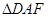
∴
∴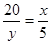
∵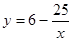
∴

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均与小正方形的顶点重合.
(1)以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且位似比为1∶2;
(2)连接(1)中的AA′,求四边形AA′C′C的周长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′;
(2)写出△A′B′C′的各顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-2,4),(2,1).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)若△ADE是△ABC关于点A的位似图形,且E的坐标为(6,-2),则点D的坐标为 , 四边形BCED面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在Rt△ABC中,AB=AC=4 .一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
(1)在整个运动过程中,设△ABC与△PQE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围;
(2)当点D在线段AB上时,连接AQ、AP,是否存在这样的t,使得△APQ成为等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由;
(3)当t=4秒时,以PQ为斜边在PQ右侧作等腰直角三角形PQF,将四边形PEQF绕点P旋转,PE与线段AB相交于点M,PF与线段AC相交于点N.试判断在这一旋转过程中,四边形PMAN的面积是否发生变化?若发生变化,求出四边形PMAN的面积y与PM的长x之间的函数关系式以及相应的自变量x的取值范围;若不发生变化,求出此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com