
如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
(1)证明见解析;(2)证明见解析;(3)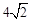 .
.
解析试题分析:(1)连接CD,由AC是⊙O的直径,可得出∠ADC=90°,由角的关系可得出∠BAC=90°,即得出EA是⊙O的切线.
(2)连接BC,由AC是⊙O的直径,可得出∠ABC=90°,由在RT△EAF中,B是EF的中点,可得出∠BAC=∠AFE,即可得出△EAF∽△CBA.
(3)由△EAF∽△CBA,可得出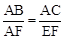 ,由比例式可求出AB,由勾股定理得出AE的长.
,由比例式可求出AB,由勾股定理得出AE的长.
试题解析:解:(1)证明:如答图1,连接CD,
∵AC是⊙O的直径,∴∠ADC=90°.
∴∠ADB+∠EDC=90°.
∵∠BAC=∠EDC,∠EAB=∠ADB,
∴∠BAC=∠EAB+∠BAC=90°.
∴EA是⊙O的切线.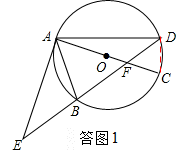
(2)证明:如答图2,连接BC,
∵AC是⊙O的直径,∴∠ABC=90°.
∴∠CBA=∠ABC=90°.
∵B是EF的中点,∴在Rt△EAF中,AB=BF.
∴∠BAC=∠AFE.∴△EAF∽△CBA.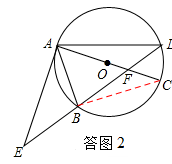
(3)∵△EAF∽△CBA,∴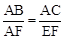 .
.
∵AF=4,CF=2,∴AC=6,EF=2AB.
∴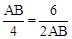 ,解得AB=
,解得AB= .∴EF=
.∴EF=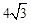 .
.
∴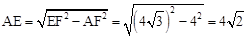 .
.
考点:1.圆周角定理;2.切线的判定;3.相似三角形的判定与性质;4.勾股定理.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
把一个三角形分割成几个小正三角形,有两种简单的“基本分割法”.
基本分割法1:如图①,把一个正三角形分割成4个小正三角形,即在原来1个正三角形的基础上增加了3个正三角形.
基本分割法2:如图②,把一个正三角形分割成6个小正三角形,即在原来1个正三角形的基础上增加了5个正三角形.
请你运用上述两种“基本分割法”,解决下列问题:
(1)把图③的正三角形分割成9个小正三角形;
(2)把图④的正三角形分割成10个小正三角形;
(3)把图⑤的正三角形分割成11个小正三角形;
(4)把图⑥的正三角形分割成12个小正三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在 中,AC=25,AB=35,
中,AC=25,AB=35, ,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
(1)如图1,当 时,求AE的长;
时,求AE的长;
(2)如图2,当点E、F在边AB上时,求
(3)联结CE,当 求
求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD•OE;
(3)若cos∠BAD=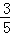 ,BE=
,BE=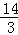 ,求OE的长.
,求OE的长.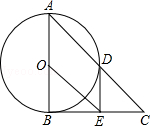
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连接AP、CE.
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当 =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当 =n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
=n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求 的值.
的值.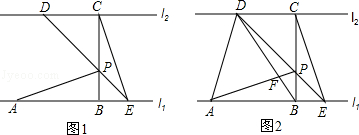
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,且DG平分△ABC的周长,设BC=a、AC=b、AB=c.
(1)求线段BG的长;
(2)求证:DG平分∠EDF;
(3)连接CG,如图2,若△GBD ∽△GDF,求证:BG⊥CG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com