
【题目】如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( ) 
A.45°
B.50°
C.60°
D.75°
科目:初中数学 来源: 题型:
【题目】如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示.AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601, ![]() ≈1.414].
≈1.414]. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙的空地上用长24m的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积S(m2). 
(1)求S与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)若墙的最大可用长度为8m,求围成花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
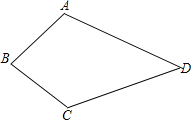
【题目】(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
(B类)已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E. 
(1)求证:MD=ME;
(2)填空:连接OE,OD,当∠A的度数为时,四边形ODME是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2 , 若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求抛物线的解析式
(1)已知抛物线的顶点为(﹣1,﹣3),与y轴的交点为(0,﹣5),求抛物线的解析式.
(2)求经过A(1,4),B(﹣2,1)两点,对称轴为x=﹣1的抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com