
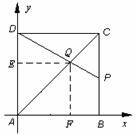
如图,在边长为4的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
(1)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有△
上何处时,都有△![]() ≌△
≌△![]() ;
;
(2)当点![]() 在
在![]() 上运动到什么位置时,△
上运动到什么位置时,△![]() 的面积是正方形
的面积是正方形![]() 面积的
面积的![]() ;
;
(3)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,当点
,在整个运动过程中,当点![]() 运动到什么位置时,△
运动到什么位置时,△![]() 恰为等腰三角形.
恰为等腰三角形.
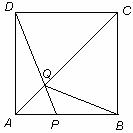
(1)证明:在正方形![]() 中,无论点
中,无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有
![]() =
=![]() ∠
∠![]() =∠
=∠![]()
![]() =
=![]()
∴△![]() ≌△
≌△![]()
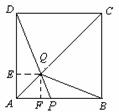
(2)解法一:△![]() 的面积恰好是正方形ABCD面积的
的面积恰好是正方形ABCD面积的![]() 时,
时,
过点Q作![]()
![]() ⊥
⊥![]() 于
于![]() ,
,![]() ⊥
⊥![]() 于
于![]() ,则
,则![]() =
= ![]()
![]()
![]() =
=![]() =
=![]()
∴![]() =
=![]()
由△![]() ∽△
∽△![]() 得
得 ![]() 解得
解得![]()
∴![]() 时,△
时,△![]() 的面积是正方形
的面积是正方形![]() 面积的
面积的![]()
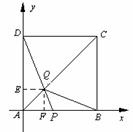
解法二:以![]() 为原点建立如图所示的直角坐标系,过点
为原点建立如图所示的直角坐标系,过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,
,![]() ⊥
⊥![]() 轴于点
轴于点![]() .
.
![]()
![]() =
=![]() =
=![]() ∴
∴![]() =
=![]()
∵点![]() 在正方形对角线
在正方形对角线![]() 上 ∴
上 ∴![]() 点的坐标为
点的坐标为![]()
∴ 过点![]() (0,4),
(0,4),![]() (
(![]() 两点的函数关系式为:
两点的函数关系式为:![]()
当![]() 时,
时,![]() ∴
∴![]() 点的坐标为(2,0)
点的坐标为(2,0)
∴![]() 时,△
时,△![]() 的面积是正方形
的面积是正方形![]() 面积的
面积的![]() .
.
(3)若△![]() 是等腰三角形,则有
是等腰三角形,则有 ![]() =
=![]() 或
或![]() =
=![]() 或
或![]() =
=![]()
①当点![]() 运动到与点
运动到与点![]() 重合时,由四边形
重合时,由四边形![]() 是正方形知
是正方形知 ![]() =
=![]()
此时△![]() 是等腰三角形
是等腰三角形
②当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 与点
与点![]() 也重合,
也重合,
此时![]() =
=![]() , △
, △![]() 是等腰三角形
是等腰三角形
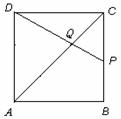
③解法一:如图,设点![]() 在
在![]() 边上运动到
边上运动到![]() 时,有
时,有![]() =
=![]()
∵ ![]() ∥
∥![]() ∴∠
∴∠![]() =∠
=∠![]()
又∵∠![]() =∠
=∠![]() ∠
∠![]() =∠
=∠![]()
∴∠![]() =∠
=∠![]()
∴ ![]() =
=![]() =
=![]()
∵![]() =
=![]()
![]() =
= ![]() =4
=4
∴![]()
即当![]() 时,△
时,△![]() 是等腰三角形
是等腰三角形
解法二:以![]() 为原点建立如图所示的直角坐标系,设点
为原点建立如图所示的直角坐标系,设点![]() 在
在![]() 上运动到
上运动到![]() 时,
时,
有![]() =
=![]() .
.
过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,
,![]() ⊥
⊥![]() 轴于点
轴于点![]() ,则
,则![]()
在![]() △
△![]() 中,
中,![]() ,∠
,∠![]() =45°
=45°
∴![]() =
=![]() °=
°=![]()
∴![]() 点的坐标为(
点的坐标为(![]() ,
,![]() )
)
∴过![]() 、
、![]() 两点的函数关系式:
两点的函数关系式:![]() +4
+4
当![]() =4时,
=4时,![]() ∴
∴![]() 点的坐标为(4,8-4
点的坐标为(4,8-4![]() ).
).
∴当点![]() 在
在![]() 上运动到
上运动到![]() 时,△
时,△![]() 是等腰三角形.
是等腰三角形.


科目:初中数学 来源: 题型:
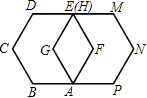 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )查看答案和解析>>
科目:初中数学 来源:初三数学圆及旋转题库 第8讲:弧长和扇形面积(解析版) 题型:解答题
 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com