
某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |

解:(1)设y与x之间的关系式为y=kx+b,由题意,得 ,解得:
,解得: 。
。
∴y= x+65。
x+65。
∵该机器生产数量至少为10台,但不超过70台,∴10≤x≤70。
(2)由题意,得xy=2000,即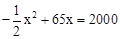 ,即
,即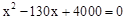 。
。
解得:x1=50,x2=80>70(舍去)。
答:该机器的生产数量为50台。
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为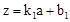 ,由函数图象,得
,由函数图象,得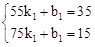 ,解得:
,解得: 。
。
∴z=﹣a+90。
当z=25时,a=65;当x=50时,y=40,
∴总利润为:25(65﹣40)=625(万元).。
答:该厂第一个月销售这种机器的利润为625万元
解析试题分析:(1)设y与x之间的关系式为y=kx+b,运用待定系数法就可以求出其关系式,由该机器生产数量至少为10台,但不超过70台就可以确定自变量的取值范围。
(2)根据每台的成本乘以生产数量等于总成本建立方程求出其解即可。
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为z=ka+b,运用待定系数法求出其解析式,再将z=25代入解析式求出a的值,就可以求出每台的利润,从而求出总利润。


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
如图,已知直线y=-x+4与反比例函数y= 的图象相交于点A(-2,a),并且与x轴相交于点B。
的图象相交于点A(-2,a),并且与x轴相交于点B。
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线y=- x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
求(1)点B'的坐标.(2)直线AM所对应的函数关系式
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知一次函数y1=kx+b与反比例函数 的图象交于A(2,4)、B(﹣4,n)两点.
的图象交于A(2,4)、B(﹣4,n)两点.
(1)分别求出y1和y2的解析式;
(2)写出y1=y2时,x的值;
(3)写出y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
| 每月用气量 | 单价(元/m3) |
| 不超出75m3的部分 | 2.5 |
| 超出75m3不超出125m3的部分 | a |
| 超出125m3的部分 | a+0.25 |
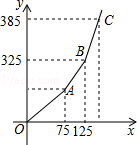
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在“美丽广西,清洁乡村”活动中,李家村村长提出了两种购买垃圾桶方案;方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元;设方案1的购买费和每月垃圾处理费共为y1元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为y2元,交费时间为x个月.
(1)直接写出y1、y2与x的函数关系式;
(2)在同一坐标系内,画出函数y1、y2的图象;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
| A.c>0 | B.2a+b=0 | C.b2﹣4ac>0 | D.a﹣b+c>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com