
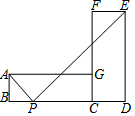
 如图,将矩形ABCG(AB<BC)绕点C顺时针旋转90°后得到矩形CFED,点P是线段BD上的一个动点,连接AP、PE,则使∠APE为直角的点P的个数是( )
如图,将矩形ABCG(AB<BC)绕点C顺时针旋转90°后得到矩形CFED,点P是线段BD上的一个动点,连接AP、PE,则使∠APE为直角的点P的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 要判断直角顶点的个数,只要判定以AE为直径的圆与线段BD的位置关系即可,相交时有2个点,相切时有1个,外离时有0个,不会出现更多的点.
解答 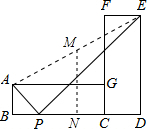 解:设两个矩形的长是a,宽是b.连接AE,如图在△AEM中,
解:设两个矩形的长是a,宽是b.连接AE,如图在△AEM中,
根据勾股定理可得:
AE2=(a+b)2+(a-b)2=2a2+2b2;
过AE的中点M作MN⊥BD于点N.则MN是梯形ABDE的中位线,
则MN=$\frac{1}{2}$(a+b);
以AE为直径的圆,半径是:$\frac{\sqrt{2({a}^{2}+{b}^{2})}}{2}$,
$\frac{1}{2}$(a+b)=$\frac{1}{2}$a+$\frac{1}{2}$b≤$\frac{\sqrt{2({a}^{2}+{b}^{2})}}{2}$,
而只有a=b是等号才成立,
因而 $\frac{1}{2}$(a+b)<$\frac{\sqrt{2({a}^{2}+{b}^{2})}}{2}$,
即圆与直线BD相交,则直角顶点P的位置有两个.
故选C.
点评 本题主要是根据直径所对的圆周角是直角,把判定顶点的个数的问题,转化为直线与圆的位置关系的问题来解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $5\frac{1}{4}{x^2}y$ | B. | yx3 | C. | ab+2 | D. | $\frac{2ab}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
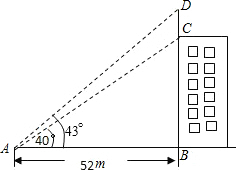 如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)
如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com