[题目]平面上.将边长相等的正三角形.正方形.正五边形.正六边形的一边重合并叠在一起.如图.则∠3+∠1﹣∠2= 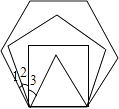．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图，则∠3+∠1﹣∠2= ．

【答案】24°
【解析】解：正三角形的每个内角是：

180°÷3=60°，

正方形的每个内角是：

360°÷4=90°，

正五边形的每个内角是：

（5﹣2）×180°÷5

=3×180°÷5

=540°÷5

=108°，

正六边形的每个内角是：

（6﹣2）×180°÷6

=4×180°÷6

=720°÷6

=120°，

则∠3+∠1﹣∠2

=（90°﹣60°）+（120°﹣108°）﹣（108°﹣90°）

=30°+12°﹣18°

=24°．

所以答案是：24°．

【考点精析】掌握多边形内角与外角和正多边形和圆是解答本题的根本，需要知道多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°；圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】填空，完成下列说理过程

如图，点A，O，B在同一条直线上， OD，OE分别平分∠AOC和∠BOC．

（1）求∠DOE的度数；

（2）如果∠COD=65°，求∠AOE的度数.

解：（1）如图，因为OD是∠AOC的平分线，

所以∠COD =∠AOC．

因为OE是∠BOC 的平分线，

所以 =∠BOC．

所以∠DOE=∠COD+ =（∠AOC+∠BOC）=∠AOB= °．

（2）由（1）可知∠BOE=∠COE = －∠COD= °.

所以∠AOE= －∠BOE = °．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，在中，平分，平分．

(1)若，则的度数为______；

(2)若，直线经过点．

①如图2，若，求的度数(用含的代数式表示)；

②如图3，若绕点旋转，分别交线段于点，试问在旋转过程中的度数是否会发生改变?若不变，求出的度数(用含的代数式表示)，若改变，请说明理由：

③如图4，继续旋转直线，与线段交于点，与的延长线交于点，请直接写出与的关系(用含的代数式表示)．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，直线m与直线n垂直相交于O，点A在直线m上运动，点B 在直线n上运动，AC、BC分别是∠BAO和∠ABO的角平分线．

（1）求∠ACB的大小；

（2）如图2，若BD是△AOB的外角∠OBE的角平分线，BD与AC相交于点D，点A、B在运动的过程中，∠ADB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；

（3）如图3，过C作直线与AB交于F，且满足∠AGO－∠BCF=45°，求证：CF∥OB．

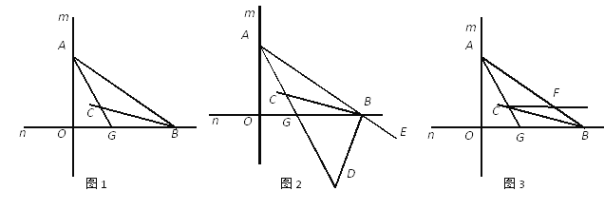
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知矩形ABCD满足AB：BC=1：，把矩形ABCD对折，使CD与AB重合，得折痕EF，把矩形ABFE绕点B逆时针旋转90°，得到矩形A′BF′E′，连结E′B，交A′F′于点M，连结AC，交EF于点N，连结AM，MN，若矩形ABCD面积为8，则△AMN的面积为（）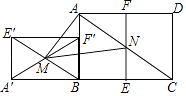

A.4
B.4
C.2
D.1

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系中，△ABC的三个顶点的位置如图所示，将△ABC水平向左平移3个单位，再竖直向下平移2个单位。

（1）读出△ABC的三个顶点坐标；

（2）请画出平移后的△A′B′C′，并直接写出点A/、B′、C′的坐标；

（3）求平移以后的图形的面积。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知四边形ABCD是菱形，在平面直角坐标系中的位置如图，边AD经过原点O，已知A（0，﹣3），B（4，0），反比例函数图象经过点C，直线AC交双曲线另一支于点E，连接DE，CD，设反比例函数解析式为y1= ，直线AC解析式为y2=ax+b．

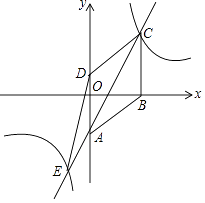
（1）求反比例函数解析式；
（2）当y1＜y2时，求x的取值范围；
（3）求△CDE的面积．