
【题目】如图1,在![]() 中,
中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,则
,则![]() 的度数为______;
的度数为______;
(2)若![]() ,直线
,直线![]() 经过点
经过点![]() .
.
①如图2,若![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 的代数式表示);
的代数式表示);
②如图3,若![]() 绕点
绕点![]() 旋转,分别交线段
旋转,分别交线段![]() 于点
于点![]() ,试问在旋转过程中
,试问在旋转过程中![]() 的度数是否会发生改变?若不变,求出
的度数是否会发生改变?若不变,求出![]() 的度数(用含
的度数(用含![]() 的代数式表示),若改变,请说明理由:
的代数式表示),若改变,请说明理由:
③如图4,继续旋转直线![]() ,与线段
,与线段![]() 交于点
交于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 的关系(用含
的关系(用含![]() 的代数式表示).
的代数式表示).

【答案】(1)130°;(2)①90![]() -
-![]() ;②不变,90
;②不变,90![]() -
-![]() ;③∠NDC+∠MDB=90
;③∠NDC+∠MDB=90![]() -
-![]() .
.
【解析】
(1)根据已知,以及三角形内角和等于180![]() ,即可求解;
,即可求解;
(2)①根据平行线的性质可以证得∠ABD=∠BDM=∠MBD,∠CND=∠A=![]() ,再利用含有
,再利用含有![]() 的式子分别表示出∠NDC、∠MDB,进行作差,即可求解代数式;
的式子分别表示出∠NDC、∠MDB,进行作差,即可求解代数式;
②延长BD交AC于点E,则∠NDE=∠MDB,因此∠NDC-∠MDB=∠NDC-∠NDE=∠EDC,再利用三角形内角和为180![]() ,即可求解;
,即可求解;
③如图可知,∠NDC+∠MDB=180![]() -∠BDC,利用平角的定义,即可求解代数式.
-∠BDC,利用平角的定义,即可求解代数式.
解:(1)∵∠A=80![]()
∴∠ABC+∠ACB=180![]() -80
-80![]() =100
=100![]()
又∵ BD平分∠ABC,CD平分∠ACB,
∴∠DBC+∠DCB=![]() 100
100![]() =50
=50![]() .
.
∴ ∠BDC=180![]() -50
-50![]() =130
=130![]() .
.
(2)①∵MN//AB,BD平分∠ABC,CD平分∠ACB,
∴∠ABD=∠BDM=∠MBD,∠CND=∠A=![]() ,
,
∴ ∠NDC=180![]() -
-![]() -
-![]() ∠ACB,∠MDB=
∠ACB,∠MDB=![]() ∠ABC,
∠ABC,
∴∠NDC-∠MDB=180![]() -
-![]() -
-![]() ∠ACB-
∠ACB-![]() ∠ABC=180
∠ABC=180![]() -
-![]() -
-![]() (∠ACB+∠ABC)=180
(∠ACB+∠ABC)=180![]() -
-![]() -
-![]() (180
(180![]() -
-![]() )=90
)=90![]() -
-![]() .
.
②不变;延长BD交AC于点E,如图:

∴∠NDE=∠MDB,
∵∠BDC=180![]() -
-![]() (∠ACB+∠ABC)=180
(∠ACB+∠ABC)=180![]() -
-![]() (180
(180![]() -
-![]() )=90
)=90![]() +
+![]() ,
,
∴∠NDC-∠MDB=∠NDC-∠NDE=∠EDC=180![]() -∠BDC=180
-∠BDC=180![]() -(90
-(90![]() +
+![]() )=90
)=90![]() -
-![]() ,
,
同①,说明MN在旋转过程中∠NDC-∠MDB的度数只与∠A有关系,而∠A始终不变,
故:MN在旋转过程中∠NDC-∠MDB的度数不会发生改变.
③如图可知,∠NDC+∠MDB=180![]() -∠BDC,
-∠BDC,
由②知∠BDC=90![]() +
+![]() ,
,
∴∠NDC+∠MDB=180![]() -(90
-(90![]() +
+![]() )=90
)=90![]() -
-![]() .
.
故∠NDC与∠MDB的关系是∠NDC+∠MDB=90![]() -
-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解答过程:
已知:如图,直线![]() ,直线
,直线![]() 与直线
与直线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ;
;![]() 平分
平分![]() ,
,![]() .求
.求![]() 的度数.
的度数.

解:![]() 与
与![]() 交于点
交于点![]() ,(已知)
,(已知)
![]() .(_______________)
.(_______________)
![]() ,(已知)
,(已知)
![]() .(______________)
.(______________)
![]() ,
,![]() 与
与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,(已知)
,(已知)
![]() (_____________)
(_____________)
![]() _______
_______![]()
![]() 平分
平分![]() ,(已知)
,(已知)
![]() _______
_______![]() .(角平分线的定义)
.(角平分线的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.
(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
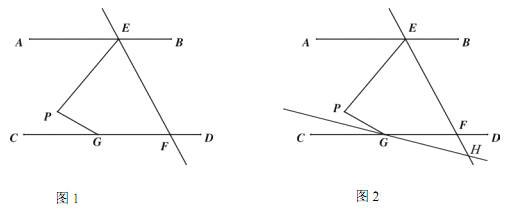
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选出两个作为补充条件,使平行四边形ABCD成为正方形(如图所示).现有下列四种选法,你认为其中错误的是( )

A. ①②B. ②④C. ①③D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为4,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S10的值为 . 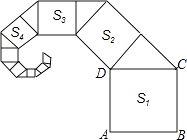
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com