
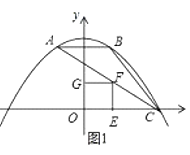
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
【答案】
(1)解:∵点B是点A关于y轴的对称点,
∴抛物线的对称轴为y轴,
∴抛物线的顶点为(0, ![]() ),
),
故抛物线的解析式可设为y=ax2+ ![]() .
.
∵A(﹣1,2)在抛物线y=ax2+ ![]() 上,
上,
∴a+ ![]() =2,
=2,
解得a=﹣ ![]() ,
,
∴抛物线的函数关系表达式为y=﹣ ![]() x2+
x2+ ![]()
(2)解:①当点F在第一象限时,如图1,
令y=0得,﹣ ![]() x2+
x2+ ![]() =0,
=0,
解得:x1=3,x2=﹣3,
∴点C的坐标为(3,0).
设直线AC的解析式为y=mx+n,
则有 ![]() ,
,
解得 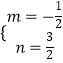 ,
,
∴直线AC的解析式为y=﹣ ![]() x+
x+ ![]() .
.
设正方形OEFG的边长为p,则F(p,p).
∵点F(p,p)在直线y=﹣ ![]() x+
x+ ![]() 上,
上,
∴﹣ ![]() p+
p+ ![]() =p,
=p,
解得p=1,
∴点F的坐标为(1,1).
②当点F在第二象限时,
同理可得:点F的坐标为(﹣3,3),
此时点F不在线段AC上,故舍去.
综上所述:点F的坐标为(1,1)
(3)解:过点M作MH⊥DN于H,如图2,

则OD=t,OE=t+1.
∵点E和点C重合时停止运动,∴0≤t≤2.
当x=t时,y=﹣ ![]() t+
t+ ![]() ,则N(t,﹣
,则N(t,﹣ ![]() t+
t+ ![]() ),DN=﹣
),DN=﹣ ![]() t+
t+ ![]() .
.
当x=t+1时,y=﹣ ![]() (t+1)+
(t+1)+ ![]() =﹣
=﹣ ![]() t+1,则M(t+1,﹣
t+1,则M(t+1,﹣ ![]() t+1),ME=﹣
t+1),ME=﹣ ![]() t+1.
t+1.
在Rt△DEM中,DM2=12+(﹣ ![]() t+1)2=
t+1)2= ![]() t2﹣t+2.
t2﹣t+2.
在Rt△NHM中,MH=1,NH=(﹣ ![]() t+
t+ ![]() )﹣(﹣
)﹣(﹣ ![]() t+1)=
t+1)= ![]() ,
,
∴MN2=12+( ![]() )2=
)2= ![]() .
.
①当DN=DM时,
(﹣ ![]() t+
t+ ![]() )2=
)2= ![]() t2﹣t+2,
t2﹣t+2,
解得t= ![]() ;
;
②当ND=NM时,
﹣ ![]() t+
t+ ![]() =
= ![]() ,
,
解得t=3﹣ ![]() ;
;
③当MN=MD时,
![]() =
= ![]() t2﹣t+2,
t2﹣t+2,
解得t1=1,t2=3.
∵0≤t≤2,∴t=1.
综上所述:当△DMN是等腰三角形时,t的值为 ![]() ,3﹣
,3﹣ ![]() 或1.
或1.
【解析】(1)根据题意可知抛物线的对称轴是y轴以及顶点为(0,94),可设抛物线解析式为y=ax2+94,利用待定系数法将A点坐标代入求出a,进而可得到抛物线解析式。
(2)由于点F为AC上一动点,因此要对点F的位置分为①当点F在第一象限;②当点F在第二象限两种情况进行讨论。先根据题意可求出直线AC的函数解析式,再设OEFG的边长为p,则F(p,p),由于点F为AC上一点,那么只要将点F代入AC的解析式中即可求出点F的坐标,注意在求得F的坐标后要验证其是否在线段AC上。
(3)过点MH⊥DN于H,根据据题意可得0≤t≤2,然后只需用t的式子表示DN、DM2、MN2,分三种情况(①DN=DM,②ND=NM,③MN=MD)建立方程,解方程讨论就可求出△DMN是等腰三角形时t的值。
【考点精析】解答此题的关键在于理解因式分解法的相关知识,掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势,以及对确定一次函数的表达式的理解,了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上, OD,OE分别平分∠AOC和∠BOC.

(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD =![]() ∠AOC.
∠AOC.
因为OE是∠BOC 的平分线,
所以 =![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知∠BOE=∠COE = -∠COD= °.
所以∠AOE= -∠BOE = °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于点P(a,b),点Q(c,d),如果a﹣b=c﹣d,那么点P与点Q就叫作等差点.例如:点P(4,2),点Q(﹣1,﹣3),因4﹣2=1﹣(﹣3)=2,则点P与点Q就是等差点.如图在矩形GHMN中,点H(2,3),点N(﹣2,﹣3),MN⊥y轴,HM⊥x轴,点P是直线y=x+b上的任意一点(点P不在矩形的边上),若矩形GHMN的边上存在两个点与点P是等差点,则b的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在四边形ABCD中,点E、点F分别为AD、BC的中点,连接EF.
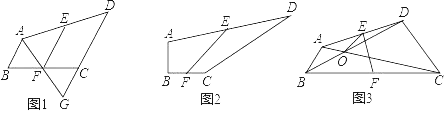
(1)如图1,AB∥CD,连接AF并延长交DC的延长线于点G,则AB、CD、EF之间的数量关系为 ;
(2)如图2,∠B=90°,∠C=150°,求AB、CD、EF之间的数量关系?
(3)如图3,∠ABC=∠BCD=45°,连接AC、BD交于点O,连接OE,若AB=![]() ,CD=2
,CD=2![]() ,BC=6,则OE= .
,BC=6,则OE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,则
,则![]() 的度数为______;
的度数为______;
(2)若![]() ,直线
,直线![]() 经过点
经过点![]() .
.
①如图2,若![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 的代数式表示);
的代数式表示);
②如图3,若![]() 绕点
绕点![]() 旋转,分别交线段
旋转,分别交线段![]() 于点
于点![]() ,试问在旋转过程中
,试问在旋转过程中![]() 的度数是否会发生改变?若不变,求出
的度数是否会发生改变?若不变,求出![]() 的度数(用含
的度数(用含![]() 的代数式表示),若改变,请说明理由:
的代数式表示),若改变,请说明理由:
③如图4,继续旋转直线![]() ,与线段
,与线段![]() 交于点
交于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 的关系(用含
的关系(用含![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
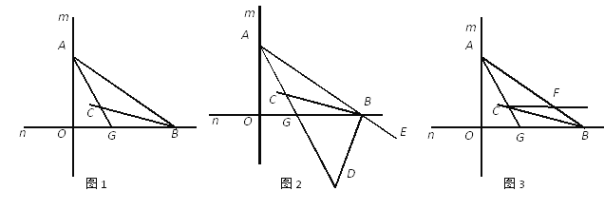
【题目】如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
(1)求∠ACB的大小;
(2)如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;
(3)如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:

(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com