
【题目】已知,在四边形ABCD中,点E、点F分别为AD、BC的中点,连接EF.
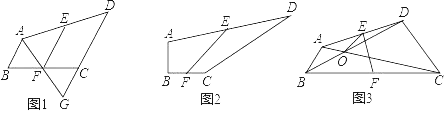
(1)如图1,AB∥CD,连接AF并延长交DC的延长线于点G,则AB、CD、EF之间的数量关系为 ;
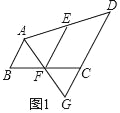
(2)如图2,∠B=90°,∠C=150°,求AB、CD、EF之间的数量关系?
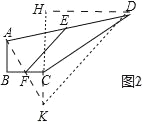
(3)如图3,∠ABC=∠BCD=45°,连接AC、BD交于点O,连接OE,若AB=![]() ,CD=2
,CD=2![]() ,BC=6,则OE= .
,BC=6,则OE= .
【答案】(1)AB+CD=2EF;(2)4EF2=AB2+CD2+ABCD,证明详见解析;(3)![]() .
.
【解析】
(1)根据三角形的中位线和全等三角形的判定和性质解答即可;
(2)如图2中,作CK⊥BC,连接AF,延长AF交CK于K.连接DK,作DH⊥CK于H.首先证明△AFB≌△KFC,推出AB=CK,再利用勾股定理,三角形的中位线定理即可解决问题;
(3)如图3中,以点B为原点,BC为x轴,建立平面直角坐标系如图所示.想办法求出点E、O的坐标即可解决问题;
解:(1)结论:AB+CD=2EF,
理由:如图1中,
∵点E、点F分别为AD、BC的中点,
∴BF=FC,AE=ED,
∵AB∥CD,
∴∠ABF=∠GCF,
∵∠BFA=∠CFG,
∴△ABF≌△GCF(ASA),
∴AB=CG,AF=FG,
∵AE=ED,AF=FG,
∴2EF=DG=DC+CG=DC+AB;
∴AB+CD=2EF;
(2)如图2中,作CK⊥BC,连接AF,延长AF交CK于K.连接DK,作DH⊥CK于H.
∵∠ABF=∠KCF,BF=FC,∠AFB=∠CFK,
∴△AFB≌△KFC,
∴AB=CK,AF=FK,
∵∠BCD=150°,∠BCK=90°,
∴∠DCK=120°,
∴∠DCH=60°,
∴CH=![]() CD,DH=
CD,DH=![]() CD,
CD,
在Rt△DKH中,DK2=DH2+KH2=(![]() CD)2+(AB+
CD)2+(AB+![]() CD)2=AB2+CD2+ABCD,
CD)2=AB2+CD2+ABCD,
∵AE=ED,AF=FK,
∴EF=![]() DK,
DK,
∴4EF2=DK2,
∴4EF2=AB2+CD2+ABCD.
(3)如图3中,以点B为原点,BC为x轴,建立平面直角坐标系如图所示.
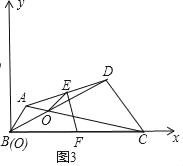
由题意:A(1,1),B(0,0),D(4,2),
∵AE=ED,
∴![]() ,
,![]() ),
),
∵AC的解析式为y=-![]() x+
x+![]() ,BD的解析式为y=
,BD的解析式为y=![]() x,
x,
由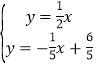 ,解得
,解得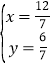 ,
,
∴O(![]() ,
,![]() ),
),
∴OE=![]() =
=![]() .
.
故答案为:(1)AB+CD=2EF;(2)4EF2=AB2+CD2+ABCD,证明详见解析;(3)![]() .
.


科目:初中数学 来源: 题型:
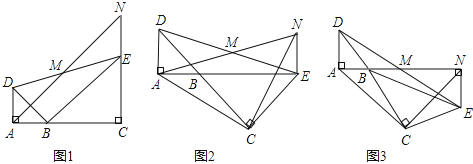
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )

A. AF=AEB. △ABE≌△AGFC. AF=EFD. BE=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选出两个作为补充条件,使平行四边形ABCD成为正方形(如图所示).现有下列四种选法,你认为其中错误的是( )

A. ①②B. ②④C. ①③D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.

已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com