
【题目】对于点P(a,b),点Q(c,d),如果a﹣b=c﹣d,那么点P与点Q就叫作等差点.例如:点P(4,2),点Q(﹣1,﹣3),因4﹣2=1﹣(﹣3)=2,则点P与点Q就是等差点.如图在矩形GHMN中,点H(2,3),点N(﹣2,﹣3),MN⊥y轴,HM⊥x轴,点P是直线y=x+b上的任意一点(点P不在矩形的边上),若矩形GHMN的边上存在两个点与点P是等差点,则b的取值范围为_____.

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,那么下列说法不正确的是( )

A. MN∥BCB. MN=AMC. AN=BCD. BM=CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解答过程:
已知:如图,直线![]() ,直线
,直线![]() 与直线
与直线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ;
;![]() 平分
平分![]() ,
,![]() .求
.求![]() 的度数.
的度数.

解:![]() 与
与![]() 交于点
交于点![]() ,(已知)
,(已知)
![]() .(_______________)
.(_______________)
![]() ,(已知)
,(已知)
![]() .(______________)
.(______________)
![]() ,
,![]() 与
与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,(已知)
,(已知)
![]() (_____________)
(_____________)
![]() _______
_______![]()
![]() 平分
平分![]() ,(已知)
,(已知)
![]() _______
_______![]() .(角平分线的定义)
.(角平分线的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选出两个作为补充条件,使平行四边形ABCD成为正方形(如图所示).现有下列四种选法,你认为其中错误的是( )

A. ①②B. ②④C. ①③D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.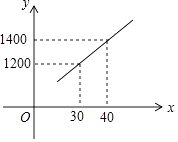
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com