
【题目】如图,将平行四边形ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,那么下列说法不正确的是( )

A. MN∥BCB. MN=AMC. AN=BCD. BM=CN
【答案】C
【解析】
根据平行四边形ABCD,可得∠B=∠D,再根据折叠可得∠D=∠NMA,再利用等量代换可得∠B=∠NMA,然后根据平行线的判定方法可得MN∥BC;首先证明四边形AMND是平行四边形,则BM=CN,AD=BC,再根据折叠可得AM=DA,则四边形AMND为菱形,再根据菱形的性质可得MN=AM.由以上可做出选择.
解:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵根据折叠可得∠D=∠NMA,
∴∠B=∠NMA,
∴MN∥BC;故A正确;
∵四边形ABCD是平行四边形,
∴DN∥AM,AD∥BC,
∵MN∥BC,
∴AD∥MN,
∴四边形AMND是平行四边形,
∴BM=CN,AD=BC,
根据折叠可得AM=DA,
∴四边形AMND为菱形,
∴MN=AM;故B、D正确;
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读材料,解决下列问题:
材料一:对非负实数x“四舍五入”到个位的值记为![]() ,即:当n为非负整数时,如果
,即:当n为非负整数时,如果![]() ,则
,则![]() ;反之,当n为非负整数时,如果
;反之,当n为非负整数时,如果![]() ;则
;则![]() ,例如:
,例如:![]() ,
,![]() ,
,![]() ,
,![]()
材料二:平面直角坐标系中任意两点![]() ,
,![]() ,我们把
,我们把![]() 叫做
叫做![]() 、
、![]() 两点间的折线距离,并规定
两点间的折线距离,并规定![]() 若
若![]() 是一定点,
是一定点,![]() 是直线
是直线![]() 上的一动点,我们把
上的一动点,我们把![]() 的最小值叫做
的最小值叫做![]() 到直线
到直线![]() 的折线距离,例如:若
的折线距离,例如:若![]() ,
,![]() 则
则![]() .
.
![]() 如果
如果![]() ,写出实数x的取值范围;
,写出实数x的取值范围;![]() 已知点
已知点![]() ,点
,点![]() ,且
,且![]() ,求a的值.
,求a的值.
![]() 若m为满足
若m为满足![]() 的最大值,求点
的最大值,求点![]() 到直线
到直线![]() 的折线距离.
的折线距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= ![]() .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
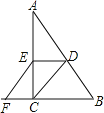
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上, OD,OE分别平分∠AOC和∠BOC.

(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD =![]() ∠AOC.
∠AOC.
因为OE是∠BOC 的平分线,
所以 =![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知∠BOE=∠COE = -∠COD= °.
所以∠AOE= -∠BOE = °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于点P(a,b),点Q(c,d),如果a﹣b=c﹣d,那么点P与点Q就叫作等差点.例如:点P(4,2),点Q(﹣1,﹣3),因4﹣2=1﹣(﹣3)=2,则点P与点Q就是等差点.如图在矩形GHMN中,点H(2,3),点N(﹣2,﹣3),MN⊥y轴,HM⊥x轴,点P是直线y=x+b上的任意一点(点P不在矩形的边上),若矩形GHMN的边上存在两个点与点P是等差点,则b的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
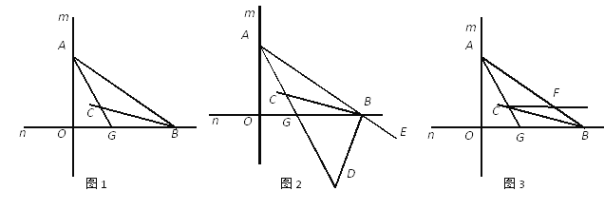
【题目】如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
(1)求∠ACB的大小;
(2)如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;
(3)如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com