
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
【答案】解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
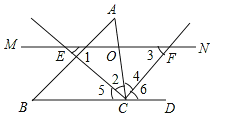
∴∠2=∠5,4=∠6。
∵MN∥BC,∴∠1=∠5,3=∠6。
∴∠1=∠2,∠3=∠4。∴EO=CO,FO=CO。
∴OE=OF。
(2)∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°。
∵CE=12,CF=5,∴![]() 。
。
∴OC=![]() EF=6.5。
EF=6.5。
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形。理由如下:
当O为AC的中点时,AO=CO,
∵EO=FO,∴四边形AECF是平行四边形。
∵∠ECF=90°,∴平行四边形AECF是矩形。
【解析】(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案。
(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可根据直角三角形斜边上的中线性质得出CO的长。
(3)根据平行四边形的判定以及矩形的判定得出即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点![]() ,
,![]() ,点
,点![]() 在第三象限,已知
在第三象限,已知![]() ,且
,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
图1
(2)如图2,![]() 为线段
为线段![]() 上一动点(端点除外),
上一动点(端点除外),![]() 是
是![]() 轴负半轴的一点,连接
轴负半轴的一点,连接![]() 、
、![]() ,射线
,射线![]() 与
与![]() 的角平分线交于
的角平分线交于![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
图2
(3)在第(2)问的基础上,如图3,点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,![]() 是射线
是射线![]() 上一个动点,连接
上一个动点,连接![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,射线
,射线![]() .试问
.试问![]() 的度数是否发生改变?若不变,请求其度数:若改变,请指出其变化范围.
的度数是否发生改变?若不变,请求其度数:若改变,请指出其变化范围.
图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,射线OC在∠A0B的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“定分线”
(1)一个角的平分线______这个角的“定分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=![]() ,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
(3)如图2,若∠MPN=45°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成90°时停止旋转,旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.当PQ是∠MPN的“定分线”时,求t的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】相传有个人不讲究说话艺术常引起误会,一天他设宴请客,他看到几个人没来,就自言自语:“怎么该来的还不来呢?”客人听了,心想难道我们是不该来的,于是已到的客人的一半走了,他一看十分着急,又说:“嗨,不该走的倒走了!”剩下的人一听,是我们该走啊!又有剩余客人的三分之一离开了,他着急地一拍大腿:“我说的不是他们.”于是剩下的6个人也走了,聪明的你知道最开始来了多少客人吗?( )
A. 16B. 18C. 20D. 22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.教育主管部门对某学校青年学校青年教师2016年度阅读情况进行了问卷调查,并将收集的数据统计如表,根据表中的信息判断,下列结论错误的是( )

A. 该学校中参与调查的青年教师人数为40人
B. 该学校中青年教师2016年平均每人阅读8本书
C. 该学校中青年教师2016年度看书数量的中位数为4本
D. 该学校中青年教师2016年度看书数量的众数为4本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D,F分别在AB,AC边上,此时BD=CF,BD⊥CF成立.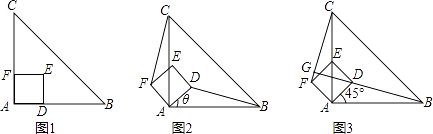
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.求证:BD⊥CF;
(3)在(2)小题的条件下,AC与BG的交点为M,当AB=4,AD= ![]() 时,求线段CM的长.
时,求线段CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,AB,BC,点E从点A出发,以每秒 ![]() 个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
(1)求抛物线的解析式;
(2)当点G落在第一象限内的抛物线上时,求出t的值;
(3)设点E从点A出发时,点E,F,G都与点A重合,点E在运动过程中,当△BCG的面积为4时,直接写出相应的t值,并直接写出点G从出发到此时所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com