
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=ax2+bx+4ΫΜy÷α”ΎΒψAΘ§≤ΔΨ≠ΙΐBΘ®4Θ§4Θ©ΚΆCΘ®6Θ§0Θ©ΝΫΒψΘ§ΒψDΒΡΉχ±ξΈΣΘ®4Θ§0Θ©Θ§Ν§Ϋ”ADΘ§ABΘ§BCΘ§ΒψE¥”ΒψA≥ωΖΔΘ§“‘ΟΩΟκ ![]() ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊœΏΕΈADœρΒψD‘ΥΕ·Θ§ΒΫ¥οΒψDΚσΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί…δœΏDC‘ΥΕ·Θ§…ηΒψEΒΡ‘ΥΕ· ±ΦδΈΣtΟκΘ§ΙΐΒψEΉςABΒΡ¥ΙœΏEFΫΜ÷±œΏAB”ΎΒψFΘ§“‘œΏΕΈEFΈΣ–±±Ώœρ”“ΉςΒ»―ϋ÷±Ϋ«ΓςEFGΘ°
ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊœΏΕΈADœρΒψD‘ΥΕ·Θ§ΒΫ¥οΒψDΚσΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί…δœΏDC‘ΥΕ·Θ§…ηΒψEΒΡ‘ΥΕ· ±ΦδΈΣtΟκΘ§ΙΐΒψEΉςABΒΡ¥ΙœΏEFΫΜ÷±œΏAB”ΎΒψFΘ§“‘œΏΕΈEFΈΣ–±±Ώœρ”“ΉςΒ»―ϋ÷±Ϋ«ΓςEFGΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Β±ΒψG¬δ‘ΎΒΎ“ΜœσœόΡΎΒΡ≈ΉΈοœΏ…œ ±Θ§«σ≥ωtΒΡ÷ΒΘΜ
Θ®3Θ©…ηΒψE¥”ΒψA≥ωΖΔ ±Θ§ΒψEΘ§FΘ§GΕΦ”κΒψA÷ΊΚœΘ§ΒψE‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§Β±ΓςBCGΒΡΟφΜΐΈΣ4 ±Θ§÷±Ϋ”–¥≥ωœύ”ΠΒΡt÷ΒΘ§≤Δ÷±Ϋ”–¥≥ωΒψG¥”≥ωΖΔΒΫ¥Υ ±ΥυΨ≠ΙΐΒΡ¬ΖΨΕ≥ΛΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚΫΪBΘ®4Θ§4Θ©ΚΆCΘ®6Θ§0Θ©¥ζ»κ≈ΉΈοœΏy=ax2+bx+4ΒΟΘΚ
![]() Θ§
Θ§
ΫβΒΟΘΚ 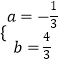 Θ§
Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=©¹ ![]() x2+
x2+ ![]() x+4
x+4
Θ®2Θ©ΫβΘΚ»γΆΦ1Θ§”…Χβ“βΒΟΘΚAE= ![]() tΘ§
tȧ 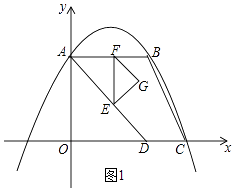
ΓΏAΘ®0Θ§4Θ©Θ§BΘ®4Θ§4Θ©Θ§
ΓύABΓΆy÷αΘ§«“ABΓΈx÷αΘ§
ΓΏOA=OD=4Θ§
ΓύΓςAOD «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύΓœADO=ΓœBAD=45ΓψΘ§
ΓύΓςAFE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύAF=EF=tΘ§
ΓΏΓςEFG «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύGΘ®t+ ![]() tΘ§4©¹
tΘ§4©¹ ![]() tΘ©Θ§
tΘ©Θ§
Φ¥ΘΚΒψGΘ® ![]() Θ§4©¹
Θ§4©¹ ![]() tΘ©Θ§
tΘ©Θ§
ΫΪΒψGΘ® ![]() Θ§4©¹
Θ§4©¹ ![]() tΘ©¥ζ»κΒΫ≈ΉΈοœΏΒΟΘΚ
tΘ©¥ζ»κΒΫ≈ΉΈοœΏΒΟΘΚ
4©¹ ![]() t=©¹
t=©¹ ![]() Θ®
Θ® ![]() Θ©2+
Θ©2+ ![]() +4Θ§
+4Θ§
ΫβΒΟΘΚt1=0Θ®…αΘ©Θ§t2= ![]() Θ§
Θ§
¥πΘΚΒ±t= ![]() ±Θ§ΒψG¬δ‘Ύ≈ΉΈοœΏ…œ
±Θ§ΒψG¬δ‘Ύ≈ΉΈοœΏ…œ
Θ®3Θ©ΫβΘΚ»γΆΦ2Θ§Ν§Ϋ”BDΘ§Β±G‘ΎBD…œ ±Θ§
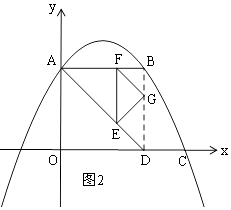
![]() =4Θ§
=4Θ§
t= ![]() Θ§
Θ§
ΔΌΒ±0ΓήtΓή ![]() ±Θ§»γΆΦ3Θ§
±Θ§»γΆΦ3Θ§ 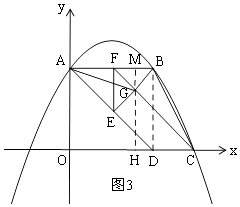
ΙΐGΉςGHΓΆx÷α”ΎHΘ§―”≥ΛHGΫΜAB”ΎMΘ§‘ρGMΓΆABΘ§
ΓΏBΘ®4Θ§4Θ©Θ§DΘ®4Θ§0Θ©Θ§
ΓύBDΓΆx÷αΘ§
ΓύSΓςBCG=SΧί–ΈGHDB+SΓςBDC©¹SΓςGHCΘ§
4= ![]() Θ®4©¹
Θ®4©¹ ![]() +4Θ©Θ®4©¹
+4Θ©Θ®4©¹ ![]() Θ©+
Θ©+ ![]() ΓΝ4ΓΝΘ®6©¹4Θ©©¹
ΓΝ4ΓΝΘ®6©¹4Θ©©¹ ![]() Θ®6©¹
Θ®6©¹ ![]() Θ©Θ®4©¹
Θ©Θ®4©¹ ![]() tΘ©Θ§
tΘ©Θ§
4= ![]() tȧ
tȧ
ΫβΒΟΘΚt= ![]() Θ§
Θ§
ΓύAM= ![]() =
= ![]() ΓΝ
ΓΝ ![]() =
= ![]() Θ§
Θ§
GM= ![]() t=
t= ![]() ΓΝ
ΓΝ ![]() =
= ![]() Θ§
Θ§
‘ΎRtΓςAGM÷–Θ§”…Ι¥Ι…Ε®άμΒΟΘΚAG= ![]() =
= ![]() =
= ![]() ΘΜ
ΘΜ
ΓύΒ±t= ![]() ±Θ§¥Υ ±ΒψG‘ΥΕ·ΒΡ¬ΖΨΕ≥ΛΈΣ
±Θ§¥Υ ±ΒψG‘ΥΕ·ΒΡ¬ΖΨΕ≥ΛΈΣ ![]() ΘΜ
ΘΜ
ΔΎΒ±G‘ΎBC…œ ±Θ§»γΆΦ4Θ§ 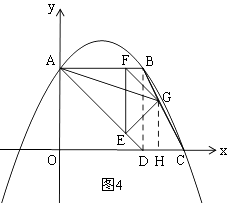
tanΓœC= ![]() =2Θ§
=2Θ§
ΓύGH=2HCΘ§
Γύ4©¹ ![]() t=2Θ®6©¹
t=2Θ®6©¹ ![]() Θ©Θ§
Θ©Θ§
t= ![]() Θ§
Θ§
Β± ![]() ΘΦtΓή
ΘΦtΓή ![]() ±Θ§»γΆΦ5Θ§
±Θ§»γΆΦ5Θ§ 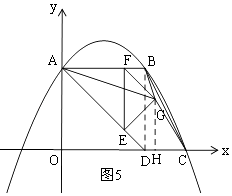
SΓςBCG=SΓςBDC©¹SΧί–ΈBDHG©¹SΓςGHCΘ§
4= ![]() ΓΝ4ΓΝ2©¹
ΓΝ4ΓΝ2©¹ ![]() Θ®4©¹
Θ®4©¹ ![]() +4Θ©Θ®
+4Θ©Θ® ![]() t©¹4Θ©©¹
t©¹4Θ©©¹ ![]() ΓΝ
ΓΝ ![]() Θ§
Θ§
t= ![]() Θ®≤Μ‘Ύ¥ΥΖΕΈßΡΎΘ§≤ΜΖϊΚœΧβ“βΘ©Θ§
Θ®≤Μ‘Ύ¥ΥΖΕΈßΡΎΘ§≤ΜΖϊΚœΧβ“βΘ©Θ§
ΔέΒ±E”κD÷ΊΚœ ±Θ§F”κB÷ΊΚœΘ§»γΆΦ6Θ§ 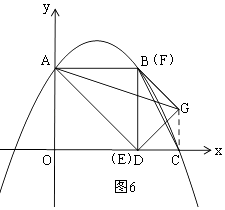
t= ![]() =4Θ§
=4Θ§
ΓύGΘ®6Θ§2Θ©Θ§
ΓύAG= ![]() =2
=2 ![]() Θ§
Θ§
ΓύSΓςBCG=SΧί–ΈBDCG©¹SΓςBDC= ![]() ΓΝ2ΓΝΘ®4+2Θ©©¹
ΓΝ2ΓΝΘ®4+2Θ©©¹ ![]() ΓΝ2ΓΝ4=2Θ§
ΓΝ2ΓΝ4=2Θ§
ΓύΒ±tΘΨ4 ±Θ§»γΆΦ7Θ§ 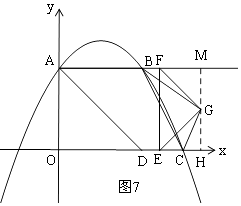
”…Χβ“βΒΟΘΚDE=t©¹4Θ§
ΓύOE=t©¹4+4=tΘ§
ΓύOH=OE+EH=t+2Θ§
EH=2Θ§GM=GH=2Θ§
BM=t+2©¹4=t©¹2Θ§
CH=t+2©¹6=t©¹4Θ§
ΙΐGΉςMHΓΆx÷αΘ§ΫΜx÷α”ΎHΘ§ΫΜ÷±œΏAB”ΎMΘ§
ΓύSΓςBGC=SΧί–ΈBCHM©¹SΓςBGM©¹SΓςGCHΘ§
4= ![]() Θ®t©¹4+t©¹2Θ©ΓΝ4©¹
Θ®t©¹4+t©¹2Θ©ΓΝ4©¹ ![]() ΓΝ2ΓΝΘ®t©¹2Θ©©¹
ΓΝ2ΓΝΘ®t©¹2Θ©©¹ ![]() ΓΝ2ΓΝΘ®t©¹4Θ©Θ§
ΓΝ2ΓΝΘ®t©¹4Θ©Θ§
t=5Θ§
Β±t=5 ±Θ§ΒψGΒΡ‘ΥΕ·¬ΖΨΕΖ÷ΈΣΝΫ≤ΩΖ÷Ήι≥…ΘΚ
iΘ©ΒψG¥”A‘ΥΕ·ΒΫD ±Θ§‘ΥΕ·¬ΖΨΕΈΣΘΚ»γΆΦ6÷–ΒΡAG≥ΛΘ§Φ¥ΈΣ2 ![]() ΘΜ
ΘΜ
iiΘ©ΒψG¥”DΒψΦΧ–χ‘Ύ…δœΏDC…œ‘ΥΕ·1Οκ ±Θ§¬ΖΨΕΈΣ1ΘΜ
Υυ“‘Β±t=5 ±Θ§¥Υ ±ΒψG‘ΥΕ·ΒΡ¬ΖΨΕ≥ΛΕ»ΈΣ1+2 ![]() Θ°
Θ°
Ήέ…œΥυ ωΘΚΒ±t1= ![]() ΟκΘ§¥Υ ±¬ΖΨΕ≥ΛΕ»ΈΣ
ΟκΘ§¥Υ ±¬ΖΨΕ≥ΛΕ»ΈΣ ![]() Θ§
Θ§
Β±t2=5ΟκΘ§¥Υ ±¬ΖΨΕ≥ΛΕ»ΈΣ1+2 ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ©άϊ”Ο¥ΐΕ®œΒ ΐΖ®Α―BΓΔCΉχ±ξ¥ζ»κΫβΈω ΫΦ¥Ω…;Θ®2Θ©”Οt ΒΡ¥ζ ΐ Ϋ±μ Ψ≥ωGΒΡΚαΉίΉχ±ξΘ§¥ζ»κ≈ΉΈοœΏΫβΈω ΫΦ¥Ω…ΘΜΘ®3Θ©t=![]() ±Θ§EΒΫDΘ§“ρ¥Υ ±Φδt Ζ÷ΈΣΒ±ΔΌ0ΓήtΓή
±Θ§EΒΫDΘ§“ρ¥Υ ±Φδt Ζ÷ΈΣΒ±ΔΌ0ΓήtΓή ![]() Θ§ ΔΎ
Θ§ ΔΎ ![]() ΘΦt
ΘΦt![]()
![]() Δέt=4 4)tΘΨ4;5).t=5 ±Θ§ΒψGΒΡ‘ΥΕ·¬ΖΨΕΖ÷ΈΣΝΫ≤ΩΖ÷Ήι≥…,ΉέΚœΤπά¥t=
Δέt=4 4)tΘΨ4;5).t=5 ±Θ§ΒψGΒΡ‘ΥΕ·¬ΖΨΕΖ÷ΈΣΝΫ≤ΩΖ÷Ήι≥…,ΉέΚœΤπά¥t=![]() Μρt=5,Ζ÷±π«σ≥ωΕ‘”ΠΒΡ¬ΖΨΕ≥Λ.
Μρt=5,Ζ÷±π«σ≥ωΕ‘”ΠΒΡ¬ΖΨΕ≥Λ.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC÷–Θ§ΒψO «±ΏAC…œ“ΜΗωΕ·ΒψΘ§ΙΐOΉς÷±œΏMNΓΈBCΘ°…ηMNΫΜΓœACBΒΡΤΫΖ÷œΏ”ΎΒψEΘ§ΫΜΓœACBΒΡΆβΫ«ΤΫΖ÷œΏ”ΎΒψFΘ°

Θ®1Θ©«σ÷ΛΘΚOE=OFΘΜ
Θ®2Θ©»τCE=12Θ§CF=5Θ§«σOCΒΡ≥ΛΘΜ
Θ®3Θ©Β±ΒψO‘Ύ±ΏAC…œ‘ΥΕ·ΒΫ ≤Ο¥ΈΜ÷Ο ±Θ§ΥΡ±Ώ–ΈAECF «ΨΊ–ΈΘΩ≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
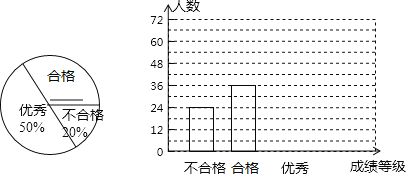
ΓΨΧβΡΩΓΩΈ“–Θ50Οϊ―ß…ζ‘ΎΡ≥“ΜΧλΒς≤ιΝΥ75ΜßΦ“ΆΞΕΣΤζΥήΝœ¥ϋΒΡ«ιΩωΘ§Ά≥ΦΤΫαΙϊ»γœ¬±μΘΚ

ΗυΨί…œ±μΜΊ¥πœ¬Ν–Έ ΧβΘΚ
(1)’βΧλΘ§“ΜΗωΦ“ΆΞ“ΜΧλΉνΕύΕΣΤζ________ΗωΥήΝœ¥ϋΘ°
(2)’βΧλΘ§ΕΣΤζ3ΗωΥήΝœ¥ϋΒΡΦ“ΆΞΜß ΐ’ΦΉήΜß ΐΒΡ________Θ°
(3)ΗΟ–ΘΥυ‘ΎΒΡΨ”Οώ«χΙ≤”–Ψ”Οώ0.8ΆρΜßΘ§‘ρΗΟ«χ“ΜΧλΕΣΤζΒΡΥήΝœ¥ϋ”–Εύ…ΌΗωΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝ≤ΡΝœΘΚ –ΓΟς‘Ύ―ßœΑΕΰ¥ΈΗυ ΫΚσΘ§ΖΔœ÷“Μ–©Κ§ΗυΚ≈ΒΡ ΫΉ”Ω…“‘–¥≥…Νμ“ΜΗω ΫΉ”ΒΡΤΫΖΫΘ§»γΘΚ![]() Θ§…Τ”ΎΥΦΩΦΒΡ–ΓΟςΫχ––ΝΥ“‘œ¬ΧΫΥςΘΚ
Θ§…Τ”ΎΥΦΩΦΒΡ–ΓΟςΫχ––ΝΥ“‘œ¬ΧΫΥςΘΚ
…η![]() Θ®Τδ÷–
Θ®Τδ÷–![]() ΨυΈΣ’ϊ ΐΘ©Θ§‘ρ”–
ΨυΈΣ’ϊ ΐΘ©Θ§‘ρ”–![]() Θ°
Θ°
Γύ![]() Θ°’β―υ–ΓΟςΨΆ’“ΒΫΝΥ“Μ÷÷Α―≤ΩΖ÷
Θ°’β―υ–ΓΟςΨΆ’“ΒΫΝΥ“Μ÷÷Α―≤ΩΖ÷![]() ΒΡ ΫΉ”Μ·ΈΣΤΫΖΫ ΫΒΡΖΫΖ®Θ°
ΒΡ ΫΉ”Μ·ΈΣΤΫΖΫ ΫΒΡΖΫΖ®Θ°
«κΡψΖ¬’’–ΓΟςΒΡΖΫΖ®ΧΫΥς≤ΔΫβΨωœ¬Ν–Έ ΧβΘΚ
Β±![]() ΨυΈΣ’ΐ’ϊ ΐ ±Θ§»τ
ΨυΈΣ’ΐ’ϊ ΐ ±Θ§»τ![]() Θ§”ΟΚ§mΓΔnΒΡ ΫΉ”Ζ÷±π±μ Ψ
Θ§”ΟΚ§mΓΔnΒΡ ΫΉ”Ζ÷±π±μ Ψ![]() Θ§ΒΟ
Θ§ΒΟ![]() ΘΫΓΓ ΓΓΘ§
ΘΫΓΓ ΓΓΘ§![]() ΘΫΓΓ ΓΓΘΜ
ΘΫΓΓ ΓΓΘΜ
Θ®2Θ©άϊ”ΟΥυΧΫΥςΒΡΫα¬έΘ§’““ΜΉι’ΐ’ϊ ΐ![]() Θ§ΧνΩ’ΘΚ ΘΪΓΓ ΓΓΘΫ(ΓΓ ΓΓΘΪΓΓ ΓΓ
Θ§ΧνΩ’ΘΚ ΘΪΓΓ ΓΓΘΫ(ΓΓ ΓΓΘΪΓΓ ΓΓ![]() )2ΘΜ
)2ΘΜ
Θ®3Θ©»τ![]() Θ§«“
Θ§«“![]() ΨυΈΣ’ΐ’ϊ ΐΘ§«σ
ΨυΈΣ’ΐ’ϊ ΐΘ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ßΕ‘»Ϊ–Θ―ß…ζΫχ––ΈΡΟςάώ“«÷Σ Ε≤β ‘Θ§ΈΣΝΥΫβ≤β ‘ΫαΙϊΘ§ΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΒΡ≥…Φ®Ϋχ––Ζ÷ΈωΘ§ΫΪ≥…Φ®Ζ÷ΈΣ»ΐΗωΒ»ΦΕΘΚ≤ΜΚœΗώΓΔΚœΗώΓΔ”≈–ψΘ§≤ΔΜφ÷Τ≥…»γœ¬ΒΡ≤ΜΆξ»ΪΆ≥ΦΤΆΦΘ°
«κΡψΗυΨίΆΦ÷–ΥυΗχΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
![]() «κΫΪ“‘…œΝΫΖυΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
«κΫΪ“‘…œΝΫΖυΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
![]() »τΓΑΚœΗώΓ±ΚΆΓΑ”≈–ψΓ±Ψυ ”ΈΣ¥ο±ξ≥…Φ®Θ§«σΗΟ–Θ±Μ≥ι»ΓΒΡ―ß…ζ÷–ΒΡ¥ο±ξ»Υ ΐΘΜ
»τΓΑΚœΗώΓ±ΚΆΓΑ”≈–ψΓ±Ψυ ”ΈΣ¥ο±ξ≥…Φ®Θ§«σΗΟ–Θ±Μ≥ι»ΓΒΡ―ß…ζ÷–ΒΡ¥ο±ξ»Υ ΐΘΜ
![]() »τΗΟ–Θ”–―ß…ζ1200»ΥΘ§«κΡψΙάΦΤ¥Υ¥Έ≤β ‘÷–Θ§»Ϊ–Θ¥ο±ξΒΡ―ß…ζ»Υ ΐΘ°
»τΗΟ–Θ”–―ß…ζ1200»ΥΘ§«κΡψΙάΦΤ¥Υ¥Έ≤β ‘÷–Θ§»Ϊ–Θ¥ο±ξΒΡ―ß…ζ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§PΈΣΖ¥±»άΐΚ· ΐy= ![]() Θ®kΘΨ0Θ©‘ΎΒΎ“ΜœσœόΡΎΆΦœσ…œΒΡ“ΜΒψΘ§ΙΐΒψPΖ÷±πΉςx÷αΘ§y÷αΒΡ¥ΙœΏΫΜ“Μ¥ΈΚ· ΐy=©¹x©¹4ΒΡΆΦœσ”ΎΒψAΘ§BΘ°»τΓœAOB=135ΓψΘ§‘ρkΒΡ÷Β «Θ® Θ©
Θ®kΘΨ0Θ©‘ΎΒΎ“ΜœσœόΡΎΆΦœσ…œΒΡ“ΜΒψΘ§ΙΐΒψPΖ÷±πΉςx÷αΘ§y÷αΒΡ¥ΙœΏΫΜ“Μ¥ΈΚ· ΐy=©¹x©¹4ΒΡΆΦœσ”ΎΒψAΘ§BΘ°»τΓœAOB=135ΓψΘ§‘ρkΒΡ÷Β «Θ® Θ©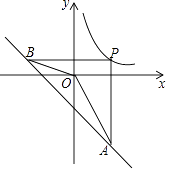
A.2
B.4
C.6
D.8
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ß≥θ“ΜΡξΦΕ”–350ΟϊΆ§―ß»Ξ¥Κ”ΈΘ§“―÷Σ2ΝΨA–Ά≥ΒΚΆ1ΝΨB–Ά≥ΒΩ…“‘‘Ί―ß…ζ100»ΥΘΜ1ΝΨA–Ά≥ΒΚΆ2ΝΨB–Ά≥ΒΩ…“‘‘Ί―ß…ζ110»ΥΘ°Θ®1Θ©AΓΔB–Ά≥ΒΟΩΝΨΩ…Ζ÷±π‘Ί―ß…ζΕύ…Ό»ΥΘΩΘ®2Θ©»τΉβ“ΜΝΨA–Ά≥Β–η“Σ1000‘ΣΘ§“ΜΝΨB–Ά≥Β–η1200‘ΣΘ§«κΡψ…ηΦΤΉβ≥ΒΖΫΑΗΘ§ ΙΒΟ«ΓΚΟ‘ΥΥΆΆξ―ß…ζ≤Δ«“Ήβ≥ΒΖ―”ΟΉν…ΌΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΤΫ––ΥΡ±Ώ–ΈΒΡ“Μ±Ώ≥ΛΈΣ7Θ§‘ρΥϋΒΡΝΫΧθΕ‘Ϋ«œΏ≥ΛΩ…“‘ «Θ®ΓΓΓΓΘ©
A. 12ΚΆ2 B. 3ΚΆ4 C. 14ΚΆ16 D. 4ΚΆ8
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§RtΓςABC÷–Θ§ΓœBACΘΫ90ΓψΘ§ABΘΫACΘ§D «BCΒΡ÷–ΒψΘ§AEΘΫBFΘ°»τBCΘΫ8Θ§‘ρΥΡ±Ώ–ΈAFDEΒΡΟφΜΐ «_____Θ°
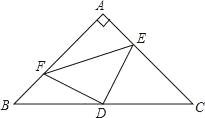
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com