
【题目】某中学初一年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.(1)A、B型车每辆可分别载学生多少人?(2)若租一辆A型车需要1000元,一辆B型车需1200元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
【答案】(1)每辆A型车可载学生30人,每辆B型车可载学生40人.(2)租1辆A型车、8辆B型车.
【解析】
(1)设每辆A型车可载学生x人,每辆B型车可载学生y人,根据“2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设租A型车m辆,租B型车n辆,根据总人数=30×租用A型车的数量+40×租用B型车的数量,即可得出关于m,n的二元一次方程,结合m,n均为正整数即可得出各租车方案,利用总钱数=每辆车的租车费用×租车数量可求出各方案所需费用,比较后即可得出结论.
解:(1)设每辆A型车可载学生x人,每辆B型车可载学生y人,
依题意,得:![]() ,
,
解得:![]() .
.
答:每辆A型车可载学生30人,每辆B型车可载学生40人.
(2)设租A型车m辆,租B型车n辆,
依题意,得:30m+40n=350,
解得:m=![]() .
.
∵m,n均为正整数,
∴![]() ,
,![]() ,
,![]() .
.
当m=9,n=2时,租车费用为1000×9+1200×2=11400(元);
当m=5,n=5时,租车费用为1000×5+1200×5=11000(元);
当m=1,n=8时,租车费用为1000×1+1200×8=10600(元).
∵11400>11000>10600,
∴租1辆A型车、8辆B型车.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.教育主管部门对某学校青年学校青年教师2016年度阅读情况进行了问卷调查,并将收集的数据统计如表,根据表中的信息判断,下列结论错误的是( )

A. 该学校中参与调查的青年教师人数为40人
B. 该学校中青年教师2016年平均每人阅读8本书
C. 该学校中青年教师2016年度看书数量的中位数为4本
D. 该学校中青年教师2016年度看书数量的众数为4本
查看答案和解析>>
科目:初中数学 来源: 题型:
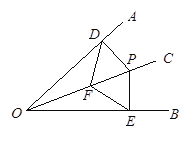
【题目】如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,AB,BC,点E从点A出发,以每秒 ![]() 个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
(1)求抛物线的解析式;
(2)当点G落在第一象限内的抛物线上时,求出t的值;
(3)设点E从点A出发时,点E,F,G都与点A重合,点E在运动过程中,当△BCG的面积为4时,直接写出相应的t值,并直接写出点G从出发到此时所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.
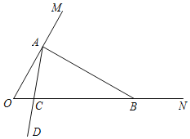
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°< ∠OAC < 90°).
(1)∠ABO的度数为 °,△AOB (填“是”或“不是”灵动三角形);
(2)若∠BAC=60°,求证:△AOC为“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
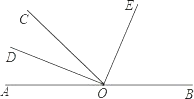
【题目】如图,O为直线AB上一点,∠AOC=50°20′,OD平分∠AOC,∠DOE=90°.
(1)求∠DOB的度数;
(2)请你通过计算说明OE是否平分∠COB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为米. (注:不计测量人员的身高,结果按四舍五入保留整数,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A,B两点,AB=18,原点O是线段AB上的一点,OA=2OB.
(1)求出A,B两点所表示的数;
(2)若点C是线段AO上一点,且满足 AC=CO+CB,求C点所表示的数;
(3)若点E以3个单位长度/秒的速度从点A沿数轴向点B方向匀速运动,同时点F以1个单位长度/秒的速度从点B沿数轴向右匀速运动,并设运动时间为t秒,问t为多少时,E、F两点重合.并求出此时数轴上所表示的数.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com