
【题目】在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.
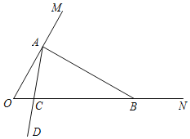
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°< ∠OAC < 90°).
(1)∠ABO的度数为 °,△AOB (填“是”或“不是”灵动三角形);
(2)若∠BAC=60°,求证:△AOC为“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
【答案】(1)30°;(2)详见解析;(3)∠OAC=80°或52.5°或30°.
【解析】
(1)根据垂直的定义、三角形内角和定理求出∠ABO的度数,根据“智慧三角形”的概念判断;
(2)根据“智慧三角形”的概念证明即可;
(3)分点C在线段OB和线段OB的延长线上两种情况,根据“智慧三角形”的定义计算.
(1)答案为:30°;是;
(2)∵AB⊥OM
∴∠BAO=90°
∵∠BAC=60°
∴∠OAC=∠BAO-∠BAC=30°
∵∠MON=60°
∴∠ACO=180°-∠OAC-∠MON=90°
∴∠ACO=3∠OAC,
∴△AOC为“灵动三角形”;
(3)设∠OAC= x°则∠BAC=90-x, ∠ACB=60+x , ∠ABC=30°
∵△ABC为“智慧三角形”,
Ⅰ、当∠ABC=3∠BAC时,°,
∴30=3(90-x), ∴x=80
Ⅱ、当∠ABC=3∠ACB时,
∴30=3(60+x) ∴x= -50 (舍去)
∴此种情况不存在,
Ⅲ、当∠BCA=3∠BAC时,
∴60+x=3(90-x),
∴x=52.5°,
Ⅳ、当∠BCA=3∠ABC时,
∴60+x=90°,
∴x=30°,
Ⅴ、当∠BAC=3∠ABC时,
∴90-x=90°,
∴x=0°(舍去)
Ⅵ、当∠BAC=3∠ACB时,
∴90-x=3(60+x),
∴x= -22.5(舍去),
∴此种情况不存在,
∴综上所述:∠OAC=80°或52.5°或30°。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y= ![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为反比例函数y= ![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是( )
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是( )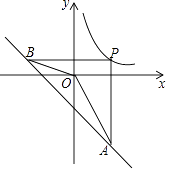
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初一年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.(1)A、B型车每辆可分别载学生多少人?(2)若租一辆A型车需要1000元,一辆B型车需1200元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形的桌子可坐6人,按下图将桌子拼起来.

按这样规律做下去:(1)有5张桌子时可坐 人;
(2)有10张桌子时可坐 人;
(3)有n张桌子可以坐 人(用含有n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
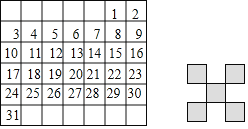
【题目】如图是某月的月历,用如图恰好能完全遮盖住月历表中的五个数字,设带阴影的“![]() ”形中的5个数字的最小数为a.
”形中的5个数字的最小数为a.
![]() 请用含a的代数式表示这5个数;
请用含a的代数式表示这5个数;
![]() 这五个数的和与“
这五个数的和与“![]() ”形中心的数有什么关系?
”形中心的数有什么关系?
![]() 盖住的5个数字的和能为105吗?为什么?
盖住的5个数字的和能为105吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )

A. 2个 B. 3个 C. 4个 D. 无数个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com