
【题目】如图,P为反比例函数y= ![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是( )
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是( )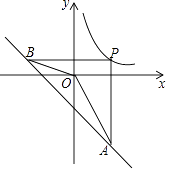
A.2
B.4
C.6
D.8
【答案】D
【解析】解:方法1、作BF⊥x轴,OE⊥AB,CQ⊥AP;设P点坐标(n, ![]() ),
),
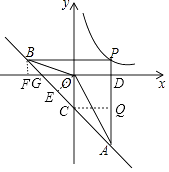
∵直线AB函数式为y=﹣x﹣4,PB⊥y轴,PA⊥x轴,
∴C(0,﹣4),G(﹣4,0),
∴OC=OG,
∴∠OGC=∠OCG=45°
∵PB∥OG,PA∥OC,
∴∠PBA=∠OGC=45°,∠PAB=∠OCG=45°,
∴PA=PB,
∵P点坐标(n, ![]() ),
),
∴OD=CQ=n,
∴AD=AQ+DQ=n+4;
∵当x=0时,y=﹣x﹣4=﹣4,
∴OC=DQ=4,GE=OE= ![]() OC=
OC= ![]() ;
;
同理可证:BG= ![]() BF=
BF= ![]() PD=
PD= ![]() ,
,
∴BE=BG+EG= ![]() +
+ ![]() ;
;
∵∠AOB=135°,
∴∠OBE+∠OAE=45°,
∵∠DAO+∠OAE=45°,
∴∠DAO=∠OBE,
∵在△BOE和△AOD中, ![]() ,
,
∴△BOE∽△AOD;
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ;
;
整理得:nk+2n2=8n+2n2,化简得:k=8;
所以答案是:D.
方法2、如图1, 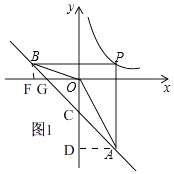
过B作BF⊥x轴于F,过点A作AD⊥y轴于D,
∵直线AB函数式为y=﹣x﹣4,PB⊥y轴,PA⊥x轴,
∴C(0,﹣4),G(﹣4,0),
∴OC=OG,
∴∠OGC=∠OCG=45°
∵PB∥OG,PA∥OC,
∴∠PBA=∠OGC=45°,∠PAB=∠OCG=45°,
∴PA=PB,
∵P点坐标(n, ![]() ),
),
∴A(n,﹣n﹣4),B(﹣4﹣ ![]() ,
, ![]() )
)
∴AD=AQ+DQ=n+4;
∵当x=0时,y=﹣x﹣4=﹣4,
∴OC=4,
当y=0时,x=﹣4.
∴OG=4,
∵∠AOB=135°,
∴∠BOG+∠AOC=45°,
∵直线AB的解析式为y=﹣x﹣4,
∴∠AGO=∠OCG=45°,
∴∠BGO=∠OCA,∠BOG+∠OBG=45°,
∴∠OBG=∠AOC,
∴△BOG∽△OAC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
在等腰Rt△BFG中,BG= ![]() BF=
BF= ![]() ,
,
在等腰Rt△ACD中,AC= ![]() AD=
AD= ![]() n,
n,
∴ ![]() ,
,
∴k=8,
所以答案是:D.
【考点精析】通过灵活运用反比例函数的图象和相似三角形的判定,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)即可以解答此题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
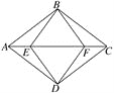
【题目】如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=AD=8,BF=6,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF,ON于点B、点C,连接AB,PB.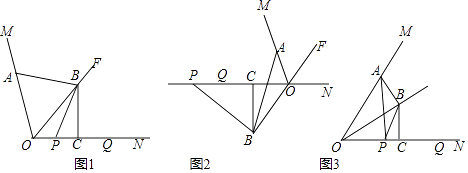
(1)如图1,当P、Q两点都在射线ON上时,请直接写出线段AB与PB的数量关系;
(2)如图2,当P、Q两点都在射线ON的反向延长线上时,线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3,∠MON=60°,连接AP,设 ![]() =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,AB,BC,点E从点A出发,以每秒 ![]() 个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
(1)求抛物线的解析式;
(2)当点G落在第一象限内的抛物线上时,求出t的值;
(3)设点E从点A出发时,点E,F,G都与点A重合,点E在运动过程中,当△BCG的面积为4时,直接写出相应的t值,并直接写出点G从出发到此时所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
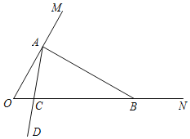
【题目】在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°< ∠OAC < 90°).
(1)∠ABO的度数为 °,△AOB (填“是”或“不是”灵动三角形);
(2)若∠BAC=60°,求证:△AOC为“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在边CD上的点F处,若△DEF的周长为8,△CBF的周长为18,则FC的长为_____.
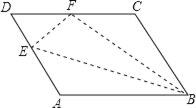
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的长度.如图2,在某一时刻,光线与水平面的夹角为72°,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,若1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆AB的长度.(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).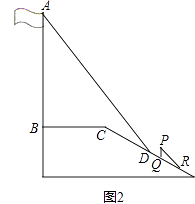
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com