
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D,F分别在AB,AC边上,此时BD=CF,BD⊥CF成立.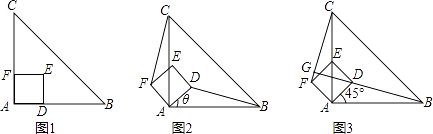
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.求证:BD⊥CF;
(3)在(2)小题的条件下,AC与BG的交点为M,当AB=4,AD= ![]() 时,求线段CM的长.
时,求线段CM的长.
【答案】
(1)解:BD=CF成立.
理由:∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∵∠BAD=∠BAC﹣∠DAC,∠CAF=∠DAF﹣∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,
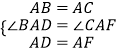 ,
,
∴△BAD≌△CAF(SAS),
∴BD=CF.
(2)证明:设BG交AC于点M,
∵△BAD≌△CAF,
∴∠ABM=∠GCM,
∵∠BMA=∠CMG,
∴△BMA∽△CMG,
∴∠BGC=∠BAC=90°,
∴BD⊥CF.
(3)解:过点F作FN⊥AC于点N,
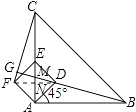
∵在正方形ADEF中,AD=DE= ![]() ,
,
∴AE= ![]() =2,
=2,
∴AN=FN= ![]() AE=1.
AE=1.
∵在等腰直角△ABC中,AB=AC=4,
∴CN=AC﹣AN=3,BC= ![]() =4
=4 ![]() ,
,
∴在Rt△FCN中,tan∠FCN= ![]() =
= ![]() ,
,
∴在Rt△ABM中,tan∠ABM= ![]() =tan∠FCN=
=tan∠FCN= ![]() ,
,
∴AM= ![]() AB=
AB= ![]() ,
,
∴CM=AC﹣AM=4﹣ ![]() =
= ![]()
【解析】(1)根据△ABC是等腰直角三角形,四边形ADEF是正方形,根据角边角关系证出△BAD≌△CAF,根据全等三角形的对应边相等,即可证得BD=CF。
(2)先设BG交AC于点M,根据(1)证出的△BAD≌△CAF,可得∠ABM=∠GCM,又根据对顶角相等,得出△BMA∽△CMG,再根据根据相似三角形的对应角相等,可得∠BGC=∠BAC=90°,即可证出BD⊥CF。
(3)首先过点F作FN⊥AC于点N,利用勾股定理即可求得AE,BC的长,继而求得AN,CN的长,又由等角的三角函数值相等,可求得AM的值,从而求出CM的值。
【考点精析】本题主要考查了等腰三角形的性质和正方形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】联想与探索:
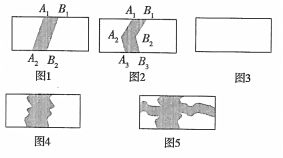
如图1,将线段A1A2本向右平移1个单位长度至B1B2,得到封闭图形A1A2B2B1(即阴影部分),在图2中,将折线A1A2A3向右平移1个单位长度至B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图3中,请你类似地画一条有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形水平方向长均为a,竖直方向长均为b) :S1= ,S2= ,S3= ;
(3)如图4,在一块长方形草地上,有一条弯曲的小路(小路任何地方的水平宽度都是2个单位长度,长方形水平方向长为a,竖直方向长为b),则空白部分表示的草地面积是多少?
(4)如图5,若在(3)中的草地上又有一条横向的曲小路(小路任何地方的宽度都是1个单位长度),则空白部分表示的草地面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y= ![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
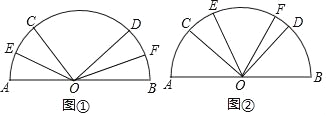
【题目】点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=100°.
(1)如图①,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数;
(2)如图②,已知∠AOC的度数为x,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校50名学生在某一天调查了75户家庭丢弃塑料袋的情况,统计结果如下表:

根据上表回答下列问题:
(1)这天,一个家庭一天最多丢弃________个塑料袋.
(2)这天,丢弃3个塑料袋的家庭户数占总户数的________.
(3)该校所在的居民区共有居民0.8万户,则该区一天丢弃的塑料袋有多少个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com