
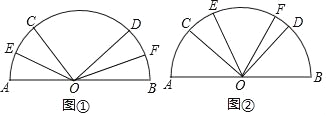
【题目】点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=100°.
(1)如图①,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数;
(2)如图②,已知∠AOC的度数为x,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.
【答案】(1)∠EOF=140°;(2)∠EOF=40°.
【解析】
(1)由角平分线的定义可得∠EOC=∠AOE=![]() ∠AOC,∠DOF=∠BOF=
∠AOC,∠DOF=∠BOF=![]() ∠BOD,则可求∠EOF的度数;
∠BOD,则可求∠EOF的度数;
(2)由题意可得∠AOD=(100+x)°,∠BOC=(180﹣x)°,由角平分线的性质可得∠DOE=![]() ∠AOD,∠COF=
∠AOD,∠COF=![]() ∠BOC,即可求∠EOF的度数.
∠BOC,即可求∠EOF的度数.
解:(1)∵OE平分∠AOC,OF平分∠BOD,
∴∠EOC=∠AOE=![]() ∠AOC,∠DOF=∠BOF=
∠AOC,∠DOF=∠BOF=![]() ∠BOD,
∠BOD,
∵∠COD=100°
∴∠AOC+∠DOB=180°﹣∠COD=80°,
∵∠EOF=∠COE+∠DOF+∠COD
∴∠EOF=![]() (∠AOC+∠BOD)+∠COD=140°
(∠AOC+∠BOD)+∠COD=140°
(2)∵∠AOC=x°
∴∠AOD=(100+x)°,∠BOC=(180﹣x)°
∵OE平分∠AOD,OF平分∠BOC,
∴∠DOE=![]() ∠AOD,∠COF=
∠AOD,∠COF=![]() ∠BOC.
∠BOC.
∵∠EOF=∠DOE+∠COF﹣∠COD
∴∠EOF=![]() (100+x+180﹣x)﹣100=40°
(100+x+180﹣x)﹣100=40°


科目:初中数学 来源: 题型:
【题目】相传有个人不讲究说话艺术常引起误会,一天他设宴请客,他看到几个人没来,就自言自语:“怎么该来的还不来呢?”客人听了,心想难道我们是不该来的,于是已到的客人的一半走了,他一看十分着急,又说:“嗨,不该走的倒走了!”剩下的人一听,是我们该走啊!又有剩余客人的三分之一离开了,他着急地一拍大腿:“我说的不是他们.”于是剩下的6个人也走了,聪明的你知道最开始来了多少客人吗?( )
A. 16B. 18C. 20D. 22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.教育主管部门对某学校青年学校青年教师2016年度阅读情况进行了问卷调查,并将收集的数据统计如表,根据表中的信息判断,下列结论错误的是( )

A. 该学校中参与调查的青年教师人数为40人
B. 该学校中青年教师2016年平均每人阅读8本书
C. 该学校中青年教师2016年度看书数量的中位数为4本
D. 该学校中青年教师2016年度看书数量的众数为4本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一批男衬衫,经过抽样调查60名中年男子,得知所需衬衫型号的人数如表所示.求出它的中位数是74,众数是76,平均数是74.6,下列说法正确的是( )

A. 所需78号人数太少,78号的可以不生产
B. 这批衬衫可以一律按身长是74.6这个平均数生产
C. 因为众数是76,故76号的生产量要占第一位
D. 因为中位数是74,故74号的生产量要占第一位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D,F分别在AB,AC边上,此时BD=CF,BD⊥CF成立.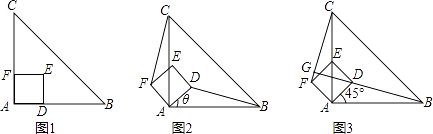
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.求证:BD⊥CF;
(3)在(2)小题的条件下,AC与BG的交点为M,当AB=4,AD= ![]() 时,求线段CM的长.
时,求线段CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
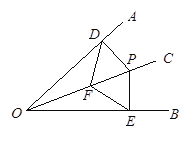
【题目】如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
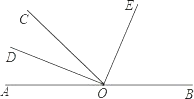
【题目】如图,O为直线AB上一点,∠AOC=50°20′,OD平分∠AOC,∠DOE=90°.
(1)求∠DOB的度数;
(2)请你通过计算说明OE是否平分∠COB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com