
����Ŀ��������̽����
��ͼ1,���߶�A1A2������ƽ��1����λ������B1B2���õ����ͼ��A1A2B2B1(����Ӱ����)����ͼ2�У�������A1A2A3����ƽ��1����λ������B1B2B3���õ����ͼ��A1A2A3B3B2B1(����Ӱ����).
(1)��ͼ3�У��������Ƶػ�һ���������۵�����ߣ�ͬ������ƽ��1����λ���ȣ��Ӷ��õ�һ�����ͼ�Σ�������Ӱ��ʾ��
(2)����ֱ�д����������ͼ���г�ȥ��Ӱ���ֺ�ʣ�ಿ�ֵ����(�賤����ˮƽ����Ϊa,��ֱ����Ϊb) ��S1= ��S2= ��S3= ;
(3)��ͼ4����һ�鳤���βݵ��ϣ���һ��������С·(С·�κεط���ˮƽ���ȶ���2����λ���ȣ�������ˮƽ����Ϊa,��ֱ����Ϊb)����հײ��ֱ�ʾ�IJݵ�����Ƕ��٣�
(4)��ͼ5������(3)�еIJݵ�������һ���������С·(С·�κεط��Ŀ��ȶ���1����λ���ȣ�����հײ��ֱ�ʾ�IJݵ�����Ƕ��٣�
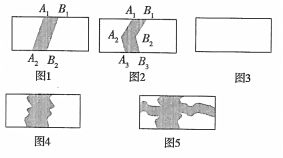
���𰸡� (1)��������(2)a(b-1)��a(b-1)��a(b-1)��(3) b(a-2)��(4)��a-2)(b-1)��
��������
��1������������ֱ�ӻ�ͼ������ע��𰸲�Ψһ��ֻҪ��һ���������۵���������õ�һ�����ͼ�μ�����
��2�����ͼ��������ƽ�Ƶ����ʿ�֪��ͼ1ͼ2ͼ3�пհײ��ֵ�������ɿ�������a��1Ϊ����bΪ���ij����ε������
��3�����ͼ����ͨ��ƽ�����հײ��ֿ�ƽ��Ϊ��a��2��Ϊ����b��Ϊ���ij����������ݳ����ε�����ɵòݵز�����ռ�������
��4�����ͼ�ο�֪���հײ�����ռ�����=��a��2����Ϊ����(b��1)��Ϊ���ij����ε������
��1����ͼ������
��2��S1=ab��b��S=ab��b��S2=ab��b��S3=ab��b
������1������С·���������������߽硰��ȥ����2�������IJݵ�����ƽ��һ����λ��3���õ�һ���µľ��������µõ��ľ����������������Ȼ��b����ˮƽ����ij������a��1�����Բݵص����������b��a��1��=ab��b��
��3��������С·�κεط���ˮƽ���ȶ���2����λ����հײ��ֱ�ʾ�IJݵ�����ǣ�a��2��b��
��4��������С·�κεط���ˮƽ���ȶ���2����λ������С·�κεط��Ŀ��ȶ���1����λ����հײ��ֱ�ʾ�IJݵ��������a��2)(b��1)��


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��PD��ֱƽ�֡�O�İ뾶OA�ڵ�B��PD����O�ڵ�C��D��PE�ǡ�O�����ߣ�EΪ�е㣬����AE����CD�ڵ�F�� 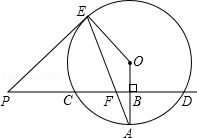
��1������O�İ뾶Ϊ8����CD�ij���
��2��֤����PE=PF��
��3����PF=13��sinA= ![]() ����EF�ij���
����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���κ���y=ax2+bx+c��a��0����ͼ����y�ύ�ڵ�C��0��4����x�ύ�ڵ�A��B����B��4��0���������ߵĶԳ���Ϊx=1��ֱ��AD���������ڵ�D��2��m����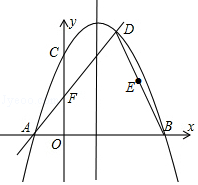
��1������κ����Ľ���ʽ��д��D�����ꣻ
��2����E��BD���е㣬��Q���߶�AB��һ���㣬����QBE�͡�ABD����ʱ�����Q�����ꣻ
��3����������y�ύ�ڵ�C��ֱ��AD��y�ύ�ڵ�F����MΪ�����߶Գ����ϵĶ��㣬��N��x���ϣ����ı���CMNF�ܳ�ȡ��Сֵʱ��������������ĵ�M�͵�N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������ѧ�һ�������˵���������ν�ϰٰ�ã����ѷּ����·ǡ������ν�ϵ�˼�뷽������ѧ��Ӧ�ü�Ϊ�㷺.
�۲����а���һ�����ɶ����ĸֹܵĺ����ͼ��
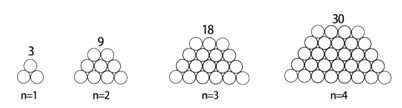
�ú�n��ʽ�ӱ�ʾ��n��ͼ�ĸֹ�����.
������˼·��
ͼ�ι����а������ֹ��ɣ����ǿ��Բ��÷ֲ��ķ���,��ͼ���������ҹ���;��ͼ�ο��ɼ������ֵ����,�����ֽṹ,�ҵ�ÿһ���ֶ�Ӧ�����ֹ���,�����ҵ�����ͼ�ζ�Ӧ�����ֹ��ɡ�
��:Ҫ����������⣬���Dz����ȴ���������:(ͳһ��S��ʾ�ֹ�����)
�����������
(1)��ͼ�������ÿ��ͼ�ΰ������������ָ�۲죬�㷢������Щ�ֹܵĶ�����������?��n=1��n=2����������,������������,������ѧ��ʽ�����㷢�ֵĹ���.

S=1+2 S=2+3+4 _____________ ______________
(2)��ʵ����ͬһ��ͼ�Σ����ǵķ����۹�����Dz�ͬ�ġ�������(1)�������ֽṹ�ġ���ÿһ������ͼ�����ӷָ��ߣ��ṩ��(1)��ͬ�ķָʽ;�������������ϣ�������ѧ��ʽ�����㷢�ֵĹ���:

_______ ____________ _______________ _______________
(3)�ú�n��ʽ����ʽ���������n��ͼ�ĸֹ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����:
(1)����4=��3����____��_____��������______��
(2)����2=��E����____��___��������____��
(3)����A=��ABE=180�㣬��____��___��������____��
(4)����2=��____����DA��EB��������____��
(5)����DBC+��_____=180�㣬��DB��EC��������____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��AOB��Rt��COD�У���AOB=��COD=90������B=40������C=60������D�ڱ�OA�ϣ���ͼ�е���COD�Ƶ�O��ÿ��10�����ٶ���˳ʱ�뷽����תһ�ܣ�����ת�Ĺ����У��ڵ� ��ʱ����CDǡ�����ABƽ�У�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������B��1��0����C��3��0����D��3��4������AΪ�����������y=ax2+bx+c����C������P�ӵ�A��������ÿ�� ![]() ����λ���ٶ����߶�AD���D�˶����˶�ʱ��Ϊt�룬����P��PE��x�ύ�������ڵ�M����AC�ڵ�N��
����λ���ٶ����߶�AD���D�˶����˶�ʱ��Ϊt�룬����P��PE��x�ύ�������ڵ�M����AC�ڵ�N��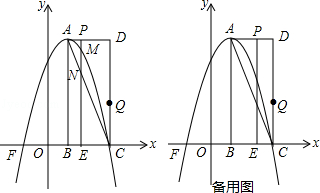
��1��ֱ��д����A�����꣬����������ߵĽ���ʽ��
��2����tΪ��ֵʱ����ACM�����������ֵΪ���٣�
��3����Q�ӵ�C��������ÿ��1����λ���ٶ����߶�CD���D�˶�����tΪ��ֵʱ�����߶�PE�ϴ��ڵ�H��ʹ��C��Q��N��HΪ������ı���Ϊ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ƽ��ֱ������ϵ�У�ֱ��y=kx+b��x�������ύ�ڵ�A����y�Ḻ���ύ�ڵ�B��Բ��P��x����������ϣ���֪AB=10��AP=![]()
��1�����P��ֱ��AB�ľ��룻
��2����ֱ��y=kx+b�Ľ���ʽ��
��3����ͼ���д��ڵ�Q��ʹ����BQO=90�㣬����AQ�������AQ����Сֵ��
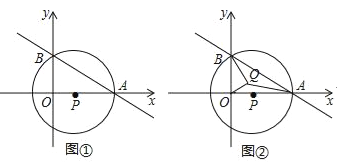
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������C��1,2���ֱ���x�ᡢy���ƽ���ߣ���ֱ��y=��x+6��A��B���㣬������������![]() ��x��0����ͼ������ABC�й����㣬��k��ȡֵ��Χ�ǣ� ��
��x��0����ͼ������ABC�й����㣬��k��ȡֵ��Χ�ǣ� ��

A. 2��k��9 B. 2��k��8 C. 2��k��5 D. 5��k��8
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com